Electrostatics
A hard copy of these problems may be downloaded.
Problems labelled A are straightforward, those marked B are supposed to be more demanding, those marked C are intended to make students think, and those marked S are synoptic.
1.1A In the Bohr model of the hydrogen atom an electron circulates the nucleus in a circular orbit of radius 52.9 pm. Calculate the electrostatic force on the electron in such an orbit.
1.2A Calculate the electrostatic force between a Na+ ion and a Cl– ion separated by 11.3 Å (i) in vacuum; (ii) in aqueous solution (εr = 78).
1.3A A HeH+ ion is slammed into a surface and loses both its electrons in the collision. The HeH+ bond length is 79 pm. Calculate the repulsive force between the two nuclei. This is called a Coulomb explosion. [cf Chem. Rev. 1980, 80, 301]
1.4A Cubic [Fe4S4] complexes are very common electron transfer centres in biological systems. In a mass spectrometer the [Fe4S4Cl4]2– complex spontaneously breaks apart into two equal fragments. The initial repulsive force between the fragments is 445 pN. Calculate the distance between the fragments at this point. [Phys. Rev. Lett. 2002, 89, 163401]
1.5B A charge +e is located at (–d/2,0,0) and a charge –e is located at (+d/2,0,0). Find the force on a charge q at the points (i) (0,0,0), (ii) (–a,0,0), (iii) (+a,0,0), (iv) (0,+a,0), (v) (0,–a,0), (vi) (a,a,a). (NB (ii) and (iii) do not simplify).
1.6B A charge q is divided into two parts. What division will maximize the repulsive force?
1.7B Three positively charged particles lie on a straight line. Their charges are q1, q2 and q3, with positions 0, x and r, respectively, so that the distances r12 = x and r23 = r – x.
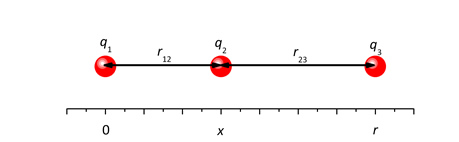
Charges 1 and 3 are fixed, charge 2 is movable.
(a) Show that at the equilibrium point for particle 2,
![]() .
.
(b) Hence show that at equilibrium
![]() .
.
(c) Show that at equilibrium the electrostatic forces on particles 1 and 3 are equal and opposite. Comment on this result.
1.8B Three charged particles lie on a straight line. Their charges are q1, q2 and q3, with positions 0, r and x, respectively, so that the distances r12 = r and r23 = x – r.
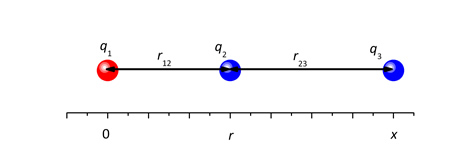
Particle 1 is positively charged and particles 2 and 3 are negatively charged. Particles 1 and 2 are fixed, particle 3 is movable.
(a) Show that at the equilibrium point for particle 3,
![]() .
.
(b) Hence show that at equilibrium,
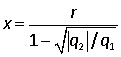 .
.
Explain the difference between the cases |q2| > q1 and |q2| < q1. Why is there no solution when |q2| = q1 ?
1.9S Suppose that the three charges in problem 1.7 are equal, and the central particle is displaced slightly along the axis from its equilibrium position. Find an expression for the restoring force on the displaced particle, and show that for a small displacement dx the restoring force is to first order
![]()
(such a particle would undergo simple harmonic motion).
2.1S Calculate the electric field experienced by
(i) the electron in problem 1.1
(ii) the chloride ion in problem 1.2
(iii) the proton in problem 1.3
(iv) one of the fragments in problem 1.4
(v) the test charge q in problem 1.5
2.2B Show that the electric field at the origin from the following charge configurations is exactly zero: (these are the partial charges on atoms in the following molecules)
(i) Two charges of –0.31e on the x axis at ±1.162 Å (O atoms in CO2).
(ii) Three charges of –0.15e equidistant from the origin at a distance of 1.307 Å, arranged in an equilateral triangle in the xy plane (F atoms in BF3).
2.3B Given the following coordinates and partial charges (for H2O) find the electric field at the point (0,0,10) Å.
Atom |
x / Å |
y / Å |
z / Å |
q/e |
O |
0.0000 |
0.0000 |
0.1173 |
-0.6568 |
H |
0.0000 |
0.7572 |
-0.4692 |
+0.3824 |
H |
0.0000 |
-0.7572 |
-0.4692 |
+0.3824 |
2.4B Sketch the electric field lines for a system of two equal and opposite charges.
2.5B In systems such those of problems 1.7 and 1.8, explain why the equilibrium position of the movable charge does not depend on the value of its charge.
2.6C In a hydrogen atom in its ground state there is a nucleus of charge +e at the origin, surrounded by an electron density
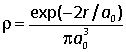
(i) Verify that this density is normalized, i.e. that
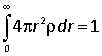
(ii) Use Gauss’s law to find the enclosed charge within a sphere of radius r, and hence the electric field in the hydrogen atom as a function of distance from the nucleus.
You may use the result
![]()
(iii) Defining an effective nuclear charge Z(r) such that
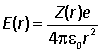
find an expression for Z(r) and sketch it.
2.7C A planar electrode has positive charge density σ per unit area on each face and is dipped into a dilute solution of an electrolyte. In the Gouy-Chapman theory of electrochemistry the electrode is surrounded by a “diffuse layer” of ions in which positive ions are repelled and negative ions are attracted. In this diffuse layer the mean charge density per unit area is –σκ exp(–κx) , where x is the distance from the electrode and κ is a constant.
(i) Explain why the electric field inside the electrode is zero.
(ii) Find an expression for the electric field as a function of distance from the surface of the electrode.
Potential energy and potential
3.1A [Prelim June 2009] (a) Write an equation for the potential energy of interaction of two ions of charge z1 and z2 in a medium of relative permittivity (dielectric constant) εr.
(b) Calculate the distance at which the coulomb interaction between ions of unit charge is equal to kT: (i) in water, εr= 78; (ii) in hexane, εr= 1.89. Assume the temperature is 298 K. Comment on the likelihood of a reaction between similarly charged ions in each solvent.
3.2A [Prelim June 2009] The ionisation energy of the K atom is 419 kJ mol–1 and the electron affinity of the Br2 molecule is 245 kJ mol–1
(a) Calculate the energy required to convert a K atom and a Br2 molecule to the ionised species K+ and Br2– at infinite separation.
(b) Calculate the separation at which the energy of attraction of the ionised species in vacuo is equal to the energy required to form them from the neutral species.
3.3A Calculate the potential energy of electrostatic interaction between a sodium ion and a chloride ion separated by 1.5 nm (i) in a vacuum, (ii) in aqueous solution (dielectric constant 80.4).
3.4A In the unit cell of a sodium chloride crystal each sodium ion is surrounded by six nearest neighbour chloride ions at a distance of 0.276 nm, twelve next nearest neighbour sodium ions at a distance of 0.390 nm and eight more chloride ions at 0.478 nm. Estimate the contribution to the potential energy of a sodium ion from interaction with each of these groups of ions.
3.5B A TV tube contains two parallel plates 7.5 mm apart. If a pd of 150 V is maintained between them
(i) calculate the electric field strength in the gap.
(ii) calculate the force on an electron in the gap.
(iii) an electron is emitted from the negative electrode with negligible velocity, calculate the time it takes to cross the gap.
3.6A The electron volt (eV) is a unit that is frequently used to measure energies on an atomic scale. One electron volt is the kinetic energy gained by an electron when it is accelerated through a potential difference of 1 V. Calculate the conversion factor from eV to J.
3.7B In the acceleration phase of a mass spectrometer positive ions are accelerated through a potential difference of 10.0 kV. Calculate the kinetic energy and the speed of (i) CH4+ and (ii) C6H6+ ions after acceleration through this field.
3.8B Two square metal plates of side 50 cm are fixed 2.0 cm apart and are maintained at a potential difference of 1.0 kV. The gap is filled with liquid cyclohexane, whose dielectric constant is 1.9.
(i) Calculate the electric field strength in the gap.
(ii) Calculate the force on a molecular singly charged cation between the plates.
(iii) Calculate the capacitance of the system and the stored charge.
3.9S A cable consists of a wire of radius r1 embedded coaxially in a dielectric cylinder with dielectric constant εr surrounded by a metal braid of radius r2. If the charge per unit length on the wire is λ, and that on the braid is –λ.
(a) Find an expression for the electric field (i) between the wire and the braid; (ii) outside the braid. Use Gauss’s law.
(b) Find an expression for the electric potential in the region between the wire and the braid. Hence deduce the potential difference between the wire and the braid and the capacitance per unit length of the cable.
4.1A Calculate the radius of a water drop with a charge –e that would remain just suspended in the earth’s electric field, 120 V m–1, which is directed downwards. Calculate also the surface charge density at the earth’s surface, and assuming the earth to be a sphere of radius 6371 km, estimate the electric charge of the earth.
4.2A Calculate the pd necessary to be maintained between two parallel plates 5.0 mm apart in order to suspend in equilibrium a small oil drop of mass 1.31×10–14 kg with an electronic charge of –2e.
4.3B A uniform electric field 500 kV m–1 acts vertically downwards. A small oil drop carrying charge –8e falls with a uniform speed of 200 mm s–1. If the charge is increased to –11e, it moves upwards with a speed of 100 mm s–1. Find
(i) the mass of the drop;
(ii) the charge it would carry if it were suspended at equilibrium in the field.
4.4C In Millikan’s experiment two consecutive measurements were as follows with a drop distance of 10.21 mm. The drop (drop 14) was timed at 18.804 s in its fall, and then when a potential difference of 5075 V was switched on between the plates separated by 16 mm, it rose through the same distance in 65.416 s. In the next measurement with the same drop the fall time was 18.662 s and the rise time 118.97 s. Calculate the charge on the drop in the two experiments and the difference between these charges. You may use the following data: T = 296.25 K, p = 100.4 kPa, η = 1.825×10–5 kg m–1 s–1, g = 9.80 m s–2, ρoil = 919.9 kg m–3, ρair = 1.2 kg m–3, b = 7.88×10–3 Pa m.
5.1A The Cl atom in the ClF3 molecule is surrounded by 5 electron pairs arranged in a trigonal bipyramid. 3 of these are bonding pairs and the remaining 2 are lone pairs. If the molecule has a non-zero dipole moment, what is its structure?
5.2B [Prelim Sept 2003] The CsCl molecule has an equilibrium internuclear distance of 360 pm. Assuming that there is complete charge transfer, calculate:
(i) its electric dipole moment in debye (D);
(ii) the coulombic contribution to the bond energy.
5.3B [Prelim June 2008] (a) Define the dipole moment of a neutral molecule.
(b) The dipole moment of SO2, a bent molecule, is 1.60 D, the bond angle is 120° and the S – O bond length is 143 pm. Determine the partial charge on each of the atoms.
5.4A The dipole moment of a C=O bond is 2.70 D and the bond length is 0.122 nm. Calculate the effective charges on the two atoms and hence estimate the percentage ionic character of the bond.
5.5A A water molecule (dipole moment 1.80 D) approaches a singly charged anion. What is the most favourable orientation of the water molecule with respect to the anion? Calculate the potential energy of the interaction at a distance of 1.0 nm and compare this to thermal kinetic energy (3kT/2) at 20°C. [The dielectric constant of water at this temperature is 80.2].
5.6S (a) Given the following coordinates and partial charges (for NH3) find the electric field at the point (0,0,10) Å.
| Atom | x / Å |
y / Å |
z / Å |
q/e |
N |
0.0000 |
0.0000 |
0.0000 |
–0.8022 |
H |
0.0000 |
–0.9377 |
–0.3816 |
+0.2674 |
H |
0.8121 |
0.4689 |
–0.3816 |
+0.2674 |
H |
–0.8121 |
0.4689 |
–0.3816 |
+0.2674 |
(b) Find the dipole moment of the molecule (repeat this for the molecule in 2.3 if you wish). Assuming this to be a point dipole at the origin, calculate the electric field at the point (0,0,10) Å. Compare this with the value you obtained in (a).
5.7B Find an expression for the energy of a dipole in a uniform electric field parallel to the z axis as a function of the angle between the dipole and the field. You may take the zero of energy to be the angle 90°.
5.8B A diatomic dipole with partial charges ±q and a separation d is oriented at an angle q relative to a constant electric field E. Find the resulting force on each atom and resolve it into components parallel to the dipole (stretching) and perpendicular to the dipole (turning).