Problems
1. In 1894 Lord Rayleigh prepared "nitrogen" by two independent methods: (a) by chemically removing the oxygen, water vapour and carbon dioxide from air, and (b) by reducing NO over hot iron. He then measured the mass (in g) of a given volume of the nitrogen so produced with the following results.
From air |
2.31017 |
2.30986 |
2.31010 |
2.31001 |
From NO |
2.30143 |
2.29890 |
2.29816 |
2.30182 |
(a) Estimate the mean and standard deviation of the mass (vapour density) measured by each method and the standard error of the mean.
(b) In your opinion is there a systematic difference between the two sets of results? Can you think of a possible reason for any difference you find?
2. The following list comprises measured values of the mass ratio of bromine and hydrogen that combine to form hydrogen bromide.
79.2863 |
79.3055 |
79.3064 |
79.3197 |
79.3114 |
79.3150 |
79.3063 |
79.3141 |
79.2915 |
79.3108 |
Calculate the sample mean M and the standard deviation S, using the two formally identical formulas. Use six digit arithmetic in each case (i.e. round each calculation to 6 significant figures at every step). Comment on the numerical difference in using the two formulas. (You might like to use Excel or some other spreadsheet that permits rounding to do this calculation).
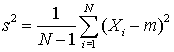 and
and 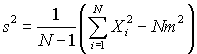
3. (i) Define the terms variance, standard error and statistical independence.
(ii) N independent measurements of a quantity are taken from an underlying distribution with mean m and standard deviation s. Show that the sum of the measurements has mean Nm and variance Ns2 and hence find an expression for the standard error of the sample mean.
1. A computer generates random numbers, which are supposed to be uniformly distributed between 0 and 1. The underlying probability density should therefore be
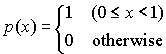
Calculate the mean and standard deviation of this distribution.
2. The probability density for the waiting time between colllisions for a molecule in a gas is given by
![]() ,
,
where w is the collision frequency.
(a) Find the expectation and variance of the waiting time T.
(b) Find an expression for the expectation E(exp(sT)). This expecation is called the moment generating function.
3. The moment generating function for a random variable T is denoted g(s) (see question 2).
(a) Show that g(0) = 1.
(b) Show that
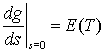 .
.
(c) Show that
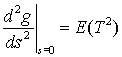 .
.
Successively higher derivatives of g give the expectations of successively higher powers of T (moments of T). Thus if the functional form of the moment generating function is known for some probability distribution, it is easy to calculate any moment desired, simply by differentiating.
4. (a) If two independent random variables, X and Y, have moment generating functions f(s) and g(s) respectively, show that the moment generating function of X+Y is f(s)xg(s).
(b) Use the results of questions 2 and 3 and part (a) to find the moment generating function for the time a molecule waits before undergoing 2 collisions in a gas; hence find the mean and standard deviation of this time.
(c) The moment generating function of a normal distribution with mean m and standard deviation s is
![]()
Show that the sum of two independent normally distributed random numbers (with different means and variances) is also normally distributed, and find expressions for the mean and variance of the sum.
1. (a) Derive the propagation of errors formula for functions of one variable.
(b) The standard Gibbs free energy change of a chemical reaction is related to the equilibrium constant by the equation
![]() .
.
An equilibrium constant is determined experimentally at 295 K to be 0.195 with a standard deviation of 0.001. Calculate the standard Gibbs free energy change for the reaction at 295 K and estimate its standard deviation.
2. When HI is heated it dissociates reversibly: HI = ½ H2+½ I2
The following values have been measured for the degree of dissociation a of HI at 629 K.
0.1953, 0.1968, 0.1956, 0.1937, 0.1949, 0.1948, 0.1954
(a) Estimate the mean and standard deviation of a and the standard error of the mean.
(b) Estimate the mean and standard error of the equilibrium constant.
3. (a) 0.400 g of NaOH (relative formula mass 39.9971) is weighed with a standard deviation of 1 mg. It is then dissolved in water and made up to 100 mL in a volumetric flask with a standard deviation of 0.5 mL. Calculate the concentration of the solution and its standard deviation.
(b) In an experiment to measure the rate constant of a reaction at 295 K, what will be the standard deviation of the rate constant arising from an uncertainty of 0.5 K in the temperature given that the activation energy is 90.00 kJ mol-1?
(c) The pH of a solution is measured to be 4.32 with a standard deviation of 0.05. What is the concentration of hydrogen ions and its standard deviation?
4. The electrolytic conductivity k is related to the measured conductance G by k = Gq, where q is the cell constant. The molar conductivity L at an experimental concentration c is given by L = k/c.
In an experiment the cell constant is 154 m-1 with a standard deviation of 1.3%, the measured conductance is 6.90 mS with a standard deviation of 0.75% and the concentration is 0.105 mol dm-3 with a standard deviation of 0.60%. Calculate the values of k and L and estimate the standard deviation in both quantities.
5. In a colorimetry experiment to determine the concentration of an inorganic complex the absorbance of the solution is measured to be 0.64 with a standard deviation of 0.03. The molar absorptivity (extinction coefficient) is 891 dm3 mol-1 cm-1 with a standard deviation of 10 dm3 mol-1 cm-1. The path length of the cell is 1 cm (and can be assumed to be without error). Calculate the concentration of the complex and estimate the experimental error in your determination.
6. The vibrational energy levels of a Morse oscillator (measured as a wavenumber) are given by the formula
![]()
where v is the vibrational quantum number. The wavenumbers for the fundamental transition and the first overtone have been measured to be 2885.0 and 5668.0 cm-1 respectively, each with a standard deviation of 0.1 cm-1.
(i)
Calculate we and wexe, and use the propagation of errors formula to estimate the standard deviation of each.
(ii) The dissociation wavenumber of a Morse oscillator is given by
![]()
Calculate the dissociation energy and estimate its standard deviation. Why is this likely to be an underestimate of the likely error?
7. (a) Use the propagation of errors formula to show that the relative error in 1/K is identical to the relative error in K.
(b) Iron (III) forms a 1:1 complex with salicylate (S) FeS2+. An experiment is carried out to measure the equilibrium constant for this reaction. This is done by measuring the concentration of the complex photometrically, and calculating the concentrations of free iron and salicylate remaining in the solution. Three different solution mixtures are made up, as tabulated below. The table contains the total concentration of iron, the total concentration of complex and the absorbance of the solution. You may assume that the errors in the tabulated concentrations are ±1%, and that the errors in the tabulated absorbance are ±2%. The molar absorptivity of the complex (extinction coefficient) is 1700 dm3 mol-1 cm-1, with an error of ±5%. You may ignore any error in the path length, which may be taken to be 1 cm exactly.
[Fe3+] / 10-4 M |
[S-]tot / 10-4 M |
A |
7.5 |
2.5 |
0.37 |
5.0 |
5.0 |
0.65 |
2.5 |
7.5 |
0.40 |
For one of the experiments (you may select which), calculate the equilibrium constant and estimate its relative error using the propagation of errors formula. To which error is the equilibrium constant most sensitive?
[The mathematics is much easier if you perform the error analysis on 1/K and use the result derived in part (a).]
8 (a) In an experiment to measure the acid dissociation constant of a weak acid by conductivity the error in the measured conductivity k arises from two independent sources: an error inherent in the measurement itself, dmk, and an error arising from uncertainty in the concentration, dck.
The second error arises because the conductivity depends on the concentration in a known way. Show that
![]()
and hence find an expression for the variance of k, the covariance of k and c and the correlation coefficient, defined as ![]()
(b) The degree of dissociation of the weak acid is related to the conductivity by a = k / cL0, where L0 is the molar conductivity at infinite dilution, and is known to have the value 3.90 S dm2 mol–1 (you may ignore any error in this value).
(i) Find an expression for the acid dissociation constant in terms of k, c and L0.
(ii) Apply the propagation of errors formula to find an expression for the variance of 1/Ka. Do not forget to include the covariance of k and c.
(iii) c is measured to be 5.0×10–3 mol dm–3, with an estimated error of 2%, and k is measured to be 113 µS cm–1, with an estimated error of 4% inherent in the measurement (excluding the error arising from the concentration). Calculate the acid dissociation constant and use the propagation of errors formula to estimate its relative error. Also calculate the correlation coefficient of k and c.