Mechanics
Speed, velocity and acceleration
Distance, velocity, acceleration and simple calculus.
1 The M25 can sustain a traffic flow of about 2400 vehicles per hour per lane at a steady speed of 60 mph (96 km/h). If the average car length is 4.6 m, what is the average spacing between cars?
2 If acceleration is constant and motion is one-dimensional, show that v2 = u2 + 2as. Interpret this formula in terms of the conservation of energy.
3 A car of length 3.5 m travelling at a speed of 20 m s−1 approaches a crossroads. The width of the intersection is 20 m. A traffic light turns to amber when the car is 50 m from the start of the intersection and turns to red 2.5 s later. If the driver brakes the car will slow down with a constant rate of 4.2 m s−2. If she accelerates the car will speed up at 1.5 m s−2. The driver wishes to avoid being photographed in the intersection while the light is red; should she brake or accelerate? Ignore the reaction time of the driver.
4 Two trains approach one another along the same track; both are travelling at 10 m s-1 but in opposite directions. They are initially 1 km apart. A fly starts at the front of one train and flies at 20 m s-1 to the other train. It then turns round and flies back to the first train again. It continues flying to and fro minding its own business until the trains crash, squashing the fly in the wreckage. How far did the fly fly before its untimely end?
5 (a) Calculate the acceleration of a particle given its time-dependent position: Position : rx(t)= αt3 where α is a constant and rx(0) =0.
(b) Calculate the time-dependent displacement of a particle, initially at rest, from its initial position given its time dependent acceleration ax(t) =6αt.
Vectors (position, velocity, acceleration).
6 The KCL Strand building has a height of 46 m. You are standing on the roof waiting to drop an egg on the Professor of Spanish, who is walking through the quad towards the gate at a constant speed of 1.20 m s−1. Where should the victim be when you release the egg?
7 A sophisticated football coach analyses the perfomance of his team using vectors. The origin is at the centre of the field, x denotes the lateral coordinate and y denotes the position downfield. The units are metres. A midfielder starts with the ball at the centre and drops back with it slowly to a position (0,−8). In the meantime a winger starting at position (9,−5) executes some complex running to find space. First he runs downfield with a displacement (0,15), then he zigs to the left, displacement (−6,4), and to the right (12,20). How far and in what direction must the midfielder pass the ball to find the winger? [Use a diagram if you wish.]
8 In the methane molecule the H atoms lie on the corners of a regular tetrahedron with the C atom at the centre. Show that a regular tetrahedron can be constructed on a unit cube by placing the H atoms at the points (1, 1, 1), (1, −1,−1), (−1, 1,−1) and (−1,−1, 1). Hence find the HCH bond angle.
9 An aircraft flies with an airspeed of 420 knots in a south-easterly direction. If the windspeed is 120 knots from the west, find the velocity of the aircraft relative to the ground.
10 In a molecular beam experiment a molecule of iodomethane is moving in the x direction with a speed of 400 m s−1 and a potassium atom is moving in the y direction with a speed of 300 m s−1. The molecules are heading for a head-on collision.
(a) Find the velocity of the centre of mass of the two molecules.
(b) Find the velocity of each molecule relative to the centre of mass.
(c) Find the momentum of each molecule relative to the centre of mass.
Comment on your answer to (c).
11 Electrons, initially travelling at 2.4 × 106 ms−1 in the horizontal direction, enter a region between two horizontal charged plates of length 2 cm where they experience an acceleration of 4 × 1014 ms−2, vertically upwards. Find
(a) the vertical position as they leave the region between the plates,
(b) the angle at which they emerge from between the plates.
12 (a) What do you understand by the term equations of motion?
(b) An electron, initially travelling with speed v0 at an angle θ to the horizontal, enters a region of length L between two parallel, horizontal charged plates, where it experiences a constant vertical acceleration, α. You may assume that the electron beam is initially directed towards the negatively charged plate. Any effects due to gravity may be neglected.
i. Write down the equations of motion for the electron.
ii. Show that the electron will enter and exit the plates at the same vertical displacement if the vertical acceleration is given by
![]()
iii. Show that under these circumstances the electron will emerge from the plates at an angle −θ to the horizontal.
Force and Momentum
1 Calculate the momentum of the following:
(a) an electron travelling at 4.0107 m s−1
(b) a nitrogen molecule travelling at 1.5102 m s−1
(c) a human of mass 60 kg running at 8.0 m s−1
2 In a TV tube an electron is accelerated from rest to a velocity of 4.0x107 m s−1 in a distance of 10 cm. Calculate the acceleration and the force on the electron.
3 A ball of mass 100 g is dropped from the top of a building of height 46 m. Calculate the force on the ball and the acceleration of the ball. How long will it take to reach the ground?
4 An aircraft of mass 20 tonne lands on an aircraft carrier deck with a horizontal velocity of 90 m s−1. If it is brought to rest in a distance of 100 m what is the average force acting on the plane? How many g of deceleration are provided?
5 The potential energy of gravitational attraction between two masses M and m is given by the formula E = −GMm/r.
(a) Find a formula for the force of attraction between the two masses.
(b) If G has the value 6.67259 10−11 N m2 kg−2, the radius of the earth is 6380 km and the acceleration due to gravity at the surface is 9.80665 m s−2, calculate the mass of the earth.
(c) What will the acceleration due to gravity be at a height of 10 km above the surface of the earth, where most jet airliners fly?
6 In the harmonic model for the vibration of a molecule the elastic potential energy stored in a stretched bond is given by
![]()
where re is the equilibrium bond length, r is the actual bond length and k is the force constant.
(a)
Find an expression for the restoring force, i.e. the force attempting to restore the molecule towards its equilibrium bond length.
(b) Sketch the variation of the elastic potential energy of the bond for a typical diatomic molecule as a function of bond extension (the potential energy curve).
(c)
Also sketch the variation of the restoring force as a function of bond extension.
(d)
On each sketch mark clearly the equilibrium bond extension.
(e)
What is the interpretation of the sign of the restoring force?
7 A shell is fired at 400 m s−1 at an angle of 30° to the horizontal.
(a) Find the horizontal and vertical components of the initial velocity.
(b) How long will the shell stay in the air (neglecting air resistance).
(c) How far from its initial position will the shell land, assuming the ground to be horizontal?
8 When a ball of effective mass m and radius a is dropped from height H in a liquid of viscosity η, two forces act on the ball: the force of gravity, −mg and a frictional drag 6ηav, where v is the velocity of the particle. The ball accelerates under the influence of gravity and as it speeds up the drag increases. The velocity where the two forces balance is called the terminal velocity. Calculate the terminal velocity as a function of the parameters given above.
9 What constant force would be required to stop each of the following objects in 0.5km:
(a) a 150 g cricket ball moving at 40 m s−1,
(b) a 13 g bullet moving at 700 m s−1,
(c) a 1500 kg car moving at 200 km h−1,
(d) a 1.8×105 kg airliner moving at 2240 km h−1?
Neglect the effects of gravity.
10 (a) State Newton’s three laws of motion, and for each law give one example of motion that illustrates it.
(b) What factors determine the trajectory of a particle in classical mechanics?
(c) A ball-bearing of mass, m, initially at rest, falls vertically under the influence of gravity through a viscous fluid, which exerts a retarding force of Cv, where C is a constant, and v is the speed of the ball-bearing. Assume that the acceleration due to gravity is a constant, g.
i. Make a sketch illustrating the forces acting on the ball-bearing and write down its equation of motion.
ii. Show that, at time t (measured from the moment of release), the speed of the ball-bearing is described by the equation
![]()
iii. Sketch the time dependence of the speed of the ball-bearing and determine its terminal speed. How would you calculate the time dependent position of the ball-bearing?
11 (a) Define the terms linear momentum and kinetic energy. How are the two quantities related? How is the change in kinetic energy related to the work done by a (conservative) force?
(b) Define the term potential energy. How is the change in potential energy related to the work done by a (conservative) force? In the light of your answer to (a), what is the significance of this result?
(c) The potential energy between two argon atoms varies with the interatomic separation, r, approximately according to the equation
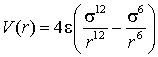
with ε =1.7 × 10−21 J and σ =3.4 × 10−10 m.
i. Sketch the variation in potential energy as a function of argon atom separation.
ii. How does the force exerted on the argon atoms vary with atomic separation? At what separations is the force between the atoms attractive and at what separations is it repulsive?
Momentum conservation and collisions
Impulse
1 A football of mass 400 g is kicked at a goalpost. It hits the post with a horizontal velocity of 30 m s−1 and rebounds with a horizontal velocity of −20 m s−1. Calculate the impulse of the force exerted by the post on the ball and the impulse of the force exerted by the ball on the post.
2 A nitrogen molecule hits a vertical wall with a velocity whose horizontal component is 300 m s−1 and rebounds with a velocity whose horizontal component is −300 m s−1.
(a) Calculate the impulse of the force exerted by the molecule on the wall.
(b) If 1.0 x 1027 such molecules hit the wall in a second, calculate the force on the wall.
Conservation of momentum and energy.
3 Rockets are propelled by ejecting the products from the combustion of rocket fuel. Suppose that at time t a rocket of mass m1 is travelling with a speed v1 and that the combustion products are ejected with a constant speed vr relative to the rocket. Find an expression for the velocity of the rocket when enough fuel has been burnt to reduce the mass to m2. You may assume that the rocket is in deep space and is unaffected by any gravitational field.
4 A 35Cl2molecule with initial velocity 600 m s−1 absorbs a photon of wavelength 350 nm and dissociates into two chlorine atoms. One atom is observed moving perpendicular to the initial direction of the molecule, with a velocity of 1600 m s−1. [Relative isotopic mass 35Cl = 34.969]
(a) Calculate the molecule’s initial kinetic energy and the photon energy.
(b) Calculate the direction and velocity of the other atom. [The momentum of the photon may be neglected.]
(c) Calculate the total kinetic energy of the fragments.
(d) Why is (c) smaller than (a)? Where has the ‘lost’ energy gone?
5 A particle of mass m travelling at a velocity v hits a stationary particle of the same mass and sticks to it. What is the final velocity, vf, of the two particles after they collide and stick together?
6 In a crossed molecular beam experiment collisions take place between molecules of 39K35Cl travelling in the +x direction at 600 m s−1 and molecules of 23Na81Br travelling in the +y direction at 400 m s−1. Find the momentum and the velocity of the resulting collision complex. [Relative isotopic masses: 39K = 38.964, 35Cl = 34.969, 23Na = 22.990, 81Br = 80.916]
Elastic collisions.
7 (a) What is meant by the term elastic collision?
(b) In a nuclear reactor the fast neutrons produced in the fission process are slowed down (moderated) by a series of elastic collisions with other nuclei. The most efficient type of collision is a head-on collision with a nucleus. Early reactors used graphite as the moderator. If a neutron with velocity 2.6 x 107 m s−1 collides with a stationary carbon nucleus,
(i) Calculate the velocities of the two particles after the collision.
(ii) How much energy has the neutron lost?
[accurate masses are not required]
(c) Carbon is not the most efficient possible moderator. What nuclear mass will maximise the energy lost by the neutron in a head-on collision?
8 (a) A snooker ball (the cue ball) travelling at 5 m s−1 hits another snooker ball (the object ball). The cue ball moves off in a direction at 37° to its original direction. Assuming the collision to be elastic calculate the speed of each ball and the direction of the object ball after the collision.
[Hint: The magnitude of the relative velocity is unchanged.]
(b)
A practical joker replaces the cue ball by a ball with the same radius but half the mass. The object ball is unchanged. Repeat the problem.
9 Two protons (H+), initially separated by a large distance r, and possessing initial velocities v = 200 m s−1, collide head-on. What is their separation of closest approach?
10 Two argon atoms (A and B) of mass m =6.6 × 10−26 kg undergo a head-on collision. Atom A has an initial speed of 400 m s−1 while the second atom B is stationary. You may assume that the interaction potential is
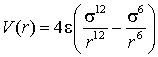
with ε =1.7 × 10−21 J and σ =3.4 × 10−10 m.
(a) What is the distance of closest approach of the two argon atoms, r0? [Use energy conservation and make the substitution x =(σ/r)6.] (b) What is the speed of the two argon atoms at r0?
(c) What is the acceleration between the atoms at r0?
(d) An elastic collision is one which conserves kinetic energy (in addition to total energy and momentum, which are conserved in all collisions). The collision between two Ar atoms is elastic. Given this fact, what are the final velocities of the atoms after the collision?
Kinetic theory of pressure and effusion (application of mechanics).
11 The rms value of the x component of the velocity of a molecule is equal to
√(RT/M), where T is the temperature and M is the mass of a mole. For the purposes of this question assume that all the molecules in a gas have velocities whose x component is √(RT/M). (See the next question for a better analysis.)
(a) Calculate this quantity for nitrogen at 298 K.
(b) The yz plane is a wall. If the number density of molecules is denoted N, find a formula for the number of molecules that hit area A of the wall in time t.
(c) Find the force on the area A and hence the pressure on the wall.
(d) The rms value of the x, y and z components of the velocity are all the same. Why? Hence find an expression for the pressure in terms of the rms value of the total velocity.
12 (For the mathematically inclined, this is a more precise version of the preceding problem.) Let the number density of molecules in a gas be N. Not all the molecules have the same velocity, consider only the x component of the molecular velocity, which is independent of the y and z components and has a probability density function f(vx). This means that the probability of a molecule having a velocity whose x component lies between vx and vx + dvx is f(vx) dvx. Consider only the small fraction of molecules in this range.
(a) How many molecules in this velocity range are there per unit volume?
(b) How many molecules in this velocity range will hit the area A in a time dt?
(c) Assuming that the molecules bounce back with a velocity −vx, calculate the contribution to the force on the wall from molecules in this range.
(d) Integrate over all possible values of vx to find the total force on the wall and hence the pressure in terms of the rms value of vx.