Rotation of a molecule
The free rotation of a rigid object with no forces acting on it is of obvious importance in chemistry. It is also a very complicated problem.
In simple examples the angular velocity is simple to interpret and remains constant throughout the rotation. This is true of a rigid object rotating about one of its principal axes, however objects rotating about an axis that is not a principal axis wobble during the course of the rotation (think about the motion of a rugby ball in flight). The result of this is that the angular velocity is not constant and the orientation of the moment of inertia is not constant either.
However, the conservation laws ensure that two quantities are constant: the angular momentum, which is given in terms of the inertial tensor as
![]()
and the rotational kinetic energy
![]()
At first sight it is hard to see how these quantities can be constant without ω also being constant. However, the first constraint (angular momentum conservation) simply ensures that the wobble in the direction of the angular velocity is counterbalanced by a wobble in the orientation of the particle such that the angular momentum is constant. The second constraint (energy conservation) ensures that the angular velocity is constrained to the surface of a wobbling ellipsoid, but that its component in the direction of the angular momentum is constant.
The equations obeyed by the angular velocity were derived by Euler in the 18th century in order to explain the wobble of the rotating earth, and an elegant geometric visualisation was derived by the mathematician Poinsot in the 19th century. The end of the angular velocity vector always lies in the plane defined by the constraint
![]()
This plane is called the invariable plane, and the motion of the angular velocity vector on this plane is called the herpolhode. The motion of the angular momentum vector in the coordinates fixed in the rotating body is called the polhode.
THE POLHODE ROLLS WITHOUT SLIPPING ON THE HERPOLHODE LYING IN THE INVARIABLE PLANE [Goldstein, Classical Mechanics, 2nd Ed. (Addison-Wesley Publishing Co., 1980).]
The motions of the polhode and the herpolhode can be very complicated, see for example the calculations on this web page.
On the other hand, if a molecule rotates about one of its principal axes none of these complications arises.
The rotational energy is given by
![]()
Using the relation between ω and L this becomes
![]()
Resolving the angular momenta along the principal axes of the moment of inertia tensor gives
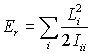
which is the equation we use to calculate the rotational energies of molecules. Notice that the energy is calculated from the angular momentum, a conserved quantity, rather than the angular velocity, which is hopelessly complicated for all but the simplest cases.