Rotational motion
This tutorial deals with the motion of a single particle in a more sophisticated way, decomposing the motion relative to some centre (the origin) into radial and angular components.
You should not try this tutorial until you have covered vectors in the maths course. Most of the vectors can be restricted to two dimensions because we will almost always be talking about rotation about a given axis, and even where we are not, as in a molecular collision, the conservation of angular momentum ensures that motion is restricted to a plane
As in the simple case of uniform motion in a circle it is useful to use polar coordinates. To this end we introduce instantaneous unit vectors in the directions of r, θ and n.

r points radially out from the centre of rotation to the rotating particle, θ is perpendicular to r and points in the tangential direction. n is a unit vector perpendicular to both r and θ.
It is straightforward geometry to see that in terms of unit vectors in the cartesian directions,

and that the position vector is simply expressed
![]()
Now we wish to resolve the velocity in these directions. The problem with this is that unit vectors in the directions r and θ change direction as time evolves, unlike the Cartesian unit vectors. To see this, differentiate the unit vectors with respect to time.
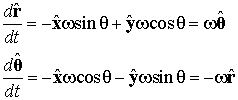
The change in the radial unit vector is therefore tangential and the change in the angular unit vector is centripetal. The angular speed ω has also been introduced by its usual formula:
![]()
Now we can resolve the velocity,
![]()
The tangential component of the velocity is given by the usual formula, but now there is also a perpendicular radial component.
The angular velocity is a vector directed along the axis of rotation in a direction defined by the right hand screw rule. Since the unit vectors in the directions r, θ and n are orthogonal it is not difficult to see that they are linked by a set of vector products:

From this we can show that

where vt is the tangential component of the velocity.
Differentiating the formula for velocity with respect to time, and remembering to take into account the time dependence of the r and θ difrections as above, we get

By Newton's second law the force is the mass of the particle times this quantity. It contains a term leading to acceleration of the radial distance, a term leading to the centripetal acceleration, both in the radial direction, and a term leading to acceleration of the angular coordinate.
A force leading to a change in ωr2 is a kind of twisting force and is usually expressed using the quantity torque.
The torque is defined as
![]()
and using our formula for acceleration this becomes
![]()
i.e. the torque is the rate of change of the angular momentum, which is a vector directed along n, the axis of rotation.
In many chemical problems there is no external force or the force is central, i.e. along the radial direction only, so that the torque is zero and the angular momentum is conserved.
The angular momentum is defined by
![]()
and in the case of our single moving particle this is
![]()
Note that the angular momentum is a vector directed along the axis of rotation, perpendicular to both the position vector and the linear momentum of the particle.
This is consistent with the statement above that torque is the rate of change of angular momentum, and if there are no external forces on the particle the angular momentum is a constant of the motion, like the linear momentum and the energy. This is particularly important, as it means that the angular momentum of an isolated molecule is fixed and the total angular momentum is constant in a molecular collision.
Ultimately the conservation of angular momentum derives from the isotropy of space (rotational symmetry, i.e. the properties of space do not depend on the direction you look in.
The kinetic energy of the particle is given by the usual formula
![]()
Using our decomposition of the velocity into radial and angular components, and remembering that the unit vectors in the directions of r and θ are orthogonal, the kinetic energy becomes
![]()
where vr is the radial component of the velocity.
The first term is the kinetic energy of rotational motion, i.e. the component from the change of the angle, and the second term is the kinetic energy of radial motion.
The rotational energy can be written in several different ways, consonant with our simple analysis of circular motion.
![]()
where I = mr2 is the moment of inertia.
An alternative useful way of writing this formula uses the angular momentum rather than the angular velocity.
![]()
For reasons that will be explained in the next topic this formula is much more useful for a rotating molecule than the previous one, and is the basis of the quantum mechanical formulation of the rotational motion.