Problems
1. (a) Identify the SI units for the following quantities and use a simple definition to express them in terms of base SI units: force, pressure, energy, power, charge, potential difference.
(b) Express each of the following fundamental constants in terms of base SI units
(i) Planck’s constant h = 6.626x10-34 J s.
(ii) The Boltzmann constant k = 1.38 x 10–23 J K–1.
(iii) The electronic charge e = 1.602x10–19 C.
(iv) The permittivity of free space e0 = 8.854x10–12 J–1 C2 m–1.
2. When a substance diffuses the flux is defined as the rate at which the amount of substance diffuses per unit area. According to Fick’s law of diffusion the flux is equal to minus the diffusion coefficient times the concentration gradient. What are the correct SI units for the flux and the concentration gradient? Hence deduce the SI units for the diffusion coefficient.
3. How many dm3 are there in one m3?
4. The universal gas constant R can be calculated from measurements of pressure, volume, temperature and amount of substance under ideal conditions from R = pV/nT.
(a) Find the SI units for R.
(b) At 298 K and 1.00 mbar pressure one mol occupies 24.8 m3. Calculate R.
(c) What is the concentration of the gas? (mol dm–3 and molec cm–3.)
5. The molar enthalpy of formation of iodine atoms is calculated from two measurable quantities: the enthalpy of sublimation of I2, which is tabulated as 60 kJ mol–1, and the bond dissociation enthalpy, which is equal to 1.5417 eV. Calculate the molar enthalpy of formation of I(g). [Don’t forget that dissociation of an iodine molecule gives two atoms.]
6. It is not permitted to take the log of a unit, so in the equation DG° =–RT ln K the equilibrium constant has no units. But the only equilibrium constants with no units are for equilibria with equal numbers of particles on each side of the equation and so the equation is only meaningful for reactions of this type. Which of the following is the best statement of the flaw in this argument?
A Units are always ignored when logarithms are taken.
B The units of K depend on the relative numbers of reactants and products in the chemical equation.
C In calculating K it is necessary to use activities instead of concentrations, and activities are dimensionless.
D There is no flaw in this argument.
Return to calculations tutorial
9. A molecule of carbon dioxide occupies a volume of 3.2 x 10-26 m3. In the British system the smallest unit of volume is the minim, which is equivalent to 0.05919385 cm3. What is the volume of the molecule in minims?
10. The speed limit on a road in Rutland is 135000 furlongs per fortnight. Given that a furlong is 1/8 mile and a fortnight is 14 days calculate the speed limit in miles per hour.
11. The slug is an American unit of mass equivalent to 14.5939 kg, and 1 foot = 30.48 cm (exactly). The density of a soil sample is 3.01 g cm-3. Convert this density to slugs per cubic foot.
12. The pressure inside a car tyre is 22 pounds (force) per square inch. Convert this to the correct SI units for pressure.
13. (a) A solution of sodium chloride has concentration 0.15 mol dm-3. Convert this concentration into molecules nm-3.
14. On the Fahrenheit temperature scale water freezes at 32°F and boils at 212°F.
(a) If the temperature is increased by 1°F, what is the increase in °C.
(b) Find absolute zero in °F.
(c) The Rankine temperature scale is the absolute version of the Fahrenheit scale, for which absolute zero is 0°R. Find the freezing point of water in °R.
(d)
The equation DG° = -RT ln K is true for any absolute temperature scale. Finf the value of the gas constant R in J mol–1 °R–1.
15. A textbook from the 1940’s uses the unit N. ft3 (normal cubic foot) for amount of substance. The normal cubic foot is defined as the amount of substance contained in 1 cubic foot of a perfect gas at a temperature of 0°C and a pressure of 1 atm. Convert this quantity to appropriate SI units. [1 foot = 30.48 cm exactly].
Return to unit conversion tutorial
16. (a) Express the SI units for density and pressure in terms of SI base units.
(b) Gas escapes through a small hole in the side of a vessel. The rate of loss of mass depends on the pressure of the gas, its density and the area of the hole.
(i) Use dimensional analysis to determine this dependence.
(ii) If the gas is perfect, how will the rate of loss depend on the molecular weight at a given pressure and temperature?
17. The speed of sound in a gas can be expressed in terms of its pressure and its density.
(a) Use dimensional analysis to determine this dependence.
(b) If the gas is perfect, how will the speed of sound depend on the molecular weight at a given temperature?
(c) The speed of sound in air at room temperature is 330 m s-1. Calculate the speed of sound in gaseous helium at the same temperature.
18. (a) When an oil droplet is released it falls under the influence of gravity until it reaches its terminal velocity at which the gravitational force exactly balances the frictional force exerted by the air through which is passes. The terminal velocity depends on the weight of the drop mg (g is the acceleration due to gravity g and m the mass) , the viscosity of the medium h and the radius of the drop a. Use dimensional analysis to work out how the terminal velocity should depend on all these factors. [The SI units for viscosity are kg m-1 s-1.]
(b) What will be the effect on the terminal velocity of the following changes?
(i) using a gas with twice the viscosity of air.
(ii) using an oil drop with double the radius.
19. The rotational energy of a diatomic molecule is a function of its bond length r, the reduced mass m, and Planck’s constant h. Use dimensional analysis to find out how the energy depends on these quantities.
20. The average speed at which an ion drifts through an electrolysis cell depends on the electric field gradient E (V m-1), the charge on the ion q (C), the viscosity of the solvent h (kg m-1 s-1) and the radius of the solvated ion a (m). Use dimensional analysis to determine this dependence. [Hint: remember that 1 V x 1 C = 1 J]
21. The van der Waals equation relating the pressure (p), volume (V) and temperature (T) of n mol of a real gas can be written:
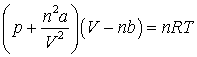
(a) Deduce the SI base units for a, b and R.
(b) The critical point of a gas is the point beyond which there is no distinction between the liquid and gas phases. For a gas that obeys the van der Waals equation the critical pressure pc, temperature Tc and molar volume Vc depend only on the three constants in the equation a, b and R. Use dimensional analysis to determine this dependence.
(c) Find combinations of a, b and R with the dimensions of pressure, molar volume and temperature and hence transform the van der Waals equation into a dimensionless form.
(d) What is the significance of the existence of such a dimensionless form?
(e) At the critical point the two equations
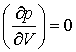
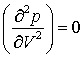
are obeyed simultaneously. Solution of these equations leads to the expression V=3b for the critical molar volume. Find the pressure, temperature and molar volume at the critical point in dimensionless units, and hence the value of pV/RT at the critical point.
22. Surface tension g measures the resistance to changing the surface area of a liquid. The energy needed to increase the surface area by DA is g DA.
(a) What are the appropriate SI base units for the surface tension?
(b) The height (h) to which a liquid will rise in a cylindrical tube by capillary action is proportional to the surface tension of the liquid (g) and also depends on its density (r), the radius of the tube (r) and the acceleration due to gravity (g). Use dimensional analysis to work out how h depends on these quantities. [This is how water is transported into plants, and how sponges soak up water.]
23. The wind-chill factor is the reduction in temperature due to the wind speed. It arises from the conversion of random motion (temperature) into organised motion (wind). The wind chill factor DT, depends on the wind speed v, the molecular mass of the gas m, and Boltzmann's constant k, which has the value 1.38x10-23 J K-1. Find the dimensions of each of these quantities and use dimensional analysis to discover how DT depends on them.
24. The terminal velocity of a spherical body falling through a liquid under gravity is proportional to g, the acceleration due to gravity, and depends on a, the radius of the sphere, r-rl, the difference between the density of the body and the density of the liquid, and h, the viscosity of the liquid (kg m-1 s-1). Find the dimensions for each of these quantities and use dimensional analysis to determine how the terminal velocity depends on them.
25. The viscosity h of a gas has the units kg m-1 s-1 and depends on the Boltzmann constant, k = 1.38 x 10-23 J K-1, the temperature, the molecular mass and the molecular diameter. Use dimensional analysis to determine how the viscosity depends on these quantities.
26. (a) The thermal wavelength of a molecule has the dimensions of length and depends on the mass of the molecule m, the Boltzmann constant kB, the absolute temperature T and Planck’s constant h. Use dimensional analysis to determine this dependence.
(b)
The discontinuity of molar entropy over a weak shock wave depends on the discontinuity in pressure, the temperature in front of the shock, and a quantity related to the compressibility of the gas, which has units m3 Pa–2 mol–1. Find this dependence using dimensional analysis.
27. The diffusion coefficient D of a gas measures the rate at which the molecules mix in a gas, and has units of m2 s–1. At a given temperature, D is inversely proportional to the pressure p of the gas and depends on the Boltzmann constant k, the temperature T, the cross-sectional area s of a molecule, and the mass m of a molecule.
(a) Express the units of each of the quantities (p, k, T, s, m ) in terms of SI base units.
(b) Use dimensional analysis to work out how D depends on these quantities.
28. The molecular collision frequency per unit concentration in a gas, Z, has units m3 s-1 and depends on the Boltzmann constant k, the temperature T, the molecular mass m and the molecular diameter d. Use dimensional analysis to determine how Z depends on these quantities.
29. (a) In a centrifugation experiment the sedimentation coefficient s is defined as
![]() '
'
where r is the radius of the circular motion, w the angular velocity and v the tangential velocity. Give the base SI units for r, w and v and hence deduce the base SI units for s. [Hint: radians are dimensionless.]
(b) The Svedberg equation relates the effective molar mass (corrected for buoyancy) M* to the universal gas constant R, the sedimentation coefficient s, the temperature T and the diffusion coefficient D, whose units are m2 s–1. Use dimensional analysis to deduce how M* is related to these quantities.
30. The electronic energy of the hydrogen atom E depends on the reduced mass of the electron m, the electronic charge e, Planck’s constant h and the permittivity of free space e0. Use dimensional analysis to work out how E depends on these quantities.
31. (a) Emin, the lowest energy possible for a molecule of mass m confined to a spherical cavity of radius r is a function of Planck’s constant, the molecular mass and the radius of the sphere. Use dimensional analysis to determine how Emin depends on these quantities.
(b) If Emin for a hydrogen atom (RAM 1.0) in a certain cavity is 3.0x10–21 J, determine Emin for a deuterium atom (RAM 2.0) in the same cavity.
32. Interstellar gas clouds above a critical mass M collapse under their own gravity. The critical mass depends on the mean molecular speed in the cloud c, the density of the cloud r, and the gravitational constant G = 6.673x10-11 m3 kg-1 s-2. Use dimensional analysis to determine how M depends on the quantities c, r and G.
33. According to Stefan’s law, the rate at which a body emits energy in the form of thermal radiation is given by sAT4, where T is the absolute temperature, A is the surface area of the body and s is known as Stefan’s constant.
(i)
What are the correct SI base units for the Stefan constant?
(ii)
Stefan’s constant depends on the Boltzmann constant k, Planck’s constant h and the speed of light c. Write down the correct SI base units for each of these quantities and use dimensional analysis to work out how s depends on these quantities.