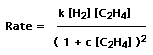
The problems are divided into two sets:
easier and
you must complete at least one from the more difficult set.
Electronic Structure
Write a program to tabulate the electronic structure of all the elements with atomic numbers from 1 to 50.
Mass Spectrometry Unknowns
Four unknown molecules are known to contain only C, N, H and O. Determine a, b, c and d in the formula CaNbHcOd, given the atomic masses (based on an old-fashioned scale) C: 12.0038, N: 14.0075, 0:16.0000, H:1.0081. The molecular masses of the molecules are 103.08, 152.11, 152.10 and 153.09; all molecules exhibit the normal rules of valency and contain less than ten carbon atoms.
Hydrogenation of Ethylene
The hydrogenation of ethylene to give ethane is symmetry-forbidden in the gas phase, but takes place readily on the clean surface of many metals. The mechanism is complex, but on a copper surface the rate of reaction is given by
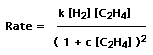
Write a program to calculate the variation in the rate with [C2H4], assuming that k=4x105, and investigate the effect of changing c in several steps from 0 to 20.
Catalysed Esterification
The rate law for a de-esterification is
![]()
in which kH+ = 4x106 dm3 mol-l s-l and kOH- = 7x107 dm3 mol-1 s-l . Write a program that calculates, tabulates logl0(Rate) as a function of pH
Rydberg Formula
The transition frequencies in the electronic spectrum of hydrogen are given by the Rydberg formula
![]()
in which RH is the Rydberg constant, 109737.32 cm-l. Write a program that determines n1 and n2 for the transitions which have frequencies 9953.50, 5503.80, 1341.23 and 359.87 cm-l. Amend your program (or write another) so that it can accept a set of several frequencies and determine whether all frequencies in a group form part of a single series (i.e. all have n1 or n2 in common).
Maxwell (Maxwell Boltzmann) Distribution of Energy
The Maxwell distribution tells us the proportion of molecules in a gas that have a given total energy. The number of molecules, dn, that have kinetic energy between E and E+dE is given by the formula
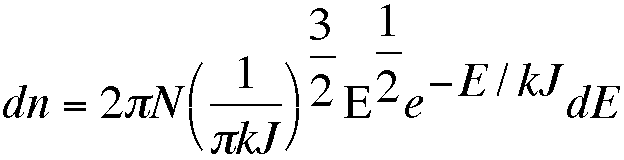
in which N is the total number of molecules and k the Boltzmann constant.
Write a program that draws the Maxwell distribution for a temperature entered from the terminal. k has the value 1.38x10-23 J K-1, and E will take values from zero to roughly 10 J. Do not attempt to integrate the equation given; instead divide the x-axis into small segments, each of width DE, and work out the value of dn for each segment before plotting.
Specific Heat of Gases
For a gas of diatomic molecules, the vibrational contribution to the specific heat is given by
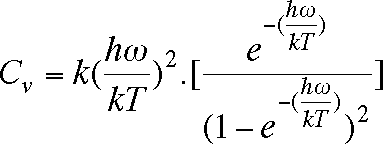
in which h (Planck's constant) = 6.626x10-34 Js, k (Boltzmann's constant) = 1.381x10-23 JK-1, T is the temperature (K) and w the vibrational frequency in Hz. Write a program that calculates and prints Cv at 100 K intervals between 100 K and 2000 K. Compare your results with the classical value Cv = k. Run your program for the following molecules, for which the vibrational frequencies are shown: Cl2 564.9; O2 1580.361; HCl 2989.74; D2 3118.4; H2 4395.2. All frequencies are given in the conventional unit, which is wavenumbers (cm-l). To convert cm-l to Hz, multiply by the speed of light, 3x1010 cm s-l.
Rotational Partition Function
Write a program to determine the rotational partition function for a diatomic molecule at temperature T.
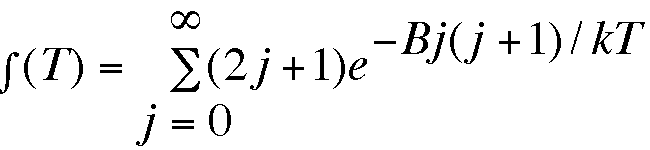
where B is the rotational constant (in cm-1) and T is the temperature (K). The Boltzmann constant k is 1.38066x10-23 JK-1 and 1000 cm-l = 1.986x10-20 J. Determine f (T) at l0K intervals from 5K to 155 K for HCl (B=15.2 cm-l ), H2 (B=85.4 cm-l), and for NO (B=2.9 cm-l), and compare with the classical approximation f (T) = T/B.
Infrared Spectrum of HCI
Write a program to draw a bar diagram of the rotational structure of the infrared spectrum of HCl at 300K. For a rigid diatomic molecule with rotational constant B, lines appear at frequencies FRJ, given by FRJ = 2B(J+l) [the "R branch"], and at FPJ = -2BJ [the "P branch"], where J is a whole number taking the values 0,1,2,3,.. [R branch] and 1,2,3,4,... [P branch] . The intensities of the lines are given by
![]()
where T is the temperature (K) and the numerical factor changes units. For HCl, B = 10-1 cm. Represent the spectrum as a series of lines or bars of height IRJ and IPJ, positioned to represent the appropriate frequency.
Laser Spectrum
Like many lasers, the output from an Argon ion (Ar+) laser consists not of a stream of photons of identical energy, but intense emission at several discrete wavelengths. Superimposed upon this line spectrum is a multitude of plasma lines which are usually several orders of magnitude less intense than the main laser lines. Laser lines have a finite, though small, bandwidth, and a shape approximating that of a Gaussian distribution
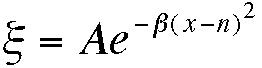
The constant b is given by b= ln(2)/(bandwidth/2)2, and a value of A (which is, for each line, proportional to the laser power) should be chosen for this problem so that the most intense peak lies just on the screen. An argon ion laser shows lines at the following wavelengths, the power for each line is shown in brackets: 488 nm (10 W), 514.5 nm (500 mW), 457.9 nm (40 mW), 476.5 nm (100 mW), 496.5 nm (100 mW). Assuming a bandwidth of 2 nm (the true bandwidth is much less than this), write a program to draw out and label the spectrum produced by an argon ion laser.
Temperature Dependence of EMF
The emf of an electrochemical cell varies with temperature (ultimately because the cell reaction involves a change in entropy.) The emf of the important cell:
Pt, H2 (g) | HCl (lM) | AgCl,Ag
varies with temperature according to the equation
E0=0.22239 - 6.455x10-3(t-25) - 3.248x10-6(t-25)2 + 9.948x10-9(t-25)3
where t is the temperature in C. Write a program that calculates the emf at 5 C intervals between 0 and 40 C and tabulates the emf and the difference between the emf at temperature t, and the emf at 25 C.
Sieve of Eratosthenes
A prime number is an integer greater than 1 whose only positive divisors are and the integer itself. One method for finding all the prime numbers in the range 2 through n is known as the Sieve of Eratosthenes. Consider the list of numbers from 2 through n. Here 2 is the first prime number, but the multiples of 2 (4, 6, 8, . . .) are not, and so they are "crossed out" in the list. The first number after 2 that was not crossed out is 3, the next prime. We then cross out all higher multiples of 3 (6, 9, 12, . . .) from the list. The next number not crossed out is 5, the next prime; we cross out all higher multiples of 5 (10, 15, 20, . . .). We repeat this procedure until we reach the first number in the list that has not been crossed out and whose square is greater than n. Then all the numbers that remain in the list are the primes from 2 through n. Write a program that uses this sieve method to find all the prime numbers from 2 through n. Run it for n = 50 and for n = 500.
Ionic Strength
The ionic strength of a solution is an important physical parameter, since it may affect the rate of reactions involving charged species. The ionic strength, I, is defined by
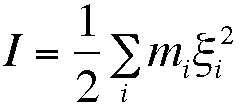
in which m is the molarity and z the charge on species i, and the sum is over all species in solution. Write a program which tabulates the ionic strength of solutions containing anions and cations with charges ranging from 1 to 4; do this as a table of size 4 by 4 in which the cations are listed as rows of the table, and anions as columns.