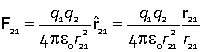Coulomb's law
Level 0 (green)- this is basic material that you have probably encountered already, although the approach may be slightly different. No prior knowledge is assumed.
Charles Augustin de Coulomb did a careful series of experiments in the 1780's, in which he measured the dependence of the electrostatic repulsion between two charged spheres as a function of distance between the spheres using a sensitive torsion balance.
There is a YouTube video of a working Coulomb torsion balance.
In the experiment shown the spheres are charged, the balance is set to a specific force and the spheres move until their repulsion equals this force. In this way Coulomb showed that the force depended inversely on the square of the distance between the spheres, like Newton's gravitational force.
Coulomb also did experiments in which an uncharged sphere is put into contact with one of the charged spheres. They then share the charge between them so that when the uncharged sphere is removed, the charge on the remaining sphere is halved, and the new force - distance relationship is found. In this way Coulomb showed that the repulsive force was symmetrical between the two spheres, and proportional to the charge on each. i.e. it didn't matter which sphere had its charge halved, and halving the charge on one sphere halves the repulsive force.
The conclusion of Coulomb's experiments was that the force between two charges q1 and q2 separated by distance r obeyed the law
![]() .
.
This equation combines the proportionality of the force to the two charges and the inverse square dependence on the separation of the charges.
In the SI unit system the Coulomb law is written
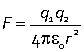
where the appropriate SI units are C (Coulomb) for the two charges, m (metre) for the distance and
![]()
ε0 is a fundamental physical constant, known as the electric constant (formerly the permittivity of free space). The units are more usually given as F m-1, which are equivalent to those given here.
The electric constant is precisely defined in terms of the magnetic constant.
Example - the force between two elementary charges
Calculate the force between two elementary charges (e.g. two protons) separated by 1.00 nm in a vacuum.
q1 = q2 = 1.602×10-19 C. r = 1.00×10-9 m. Hence F = 2.31×10-10 N.
Force is a vector.The Coulomb force is directed along the vector joining the two interacting particles. |
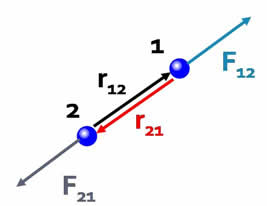 |
| The direction of the force depends on the signs of the charges. | |
| If the charges have the same sign the forces are in the same direction as the interparticle vectors, i.e. repulsive. | 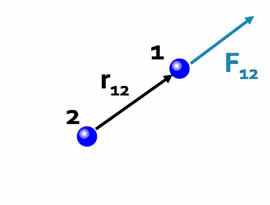 |
| If the charges have the opposite sign, the forces are antiparallel to the interparticle vectors, i.e. attractive. | 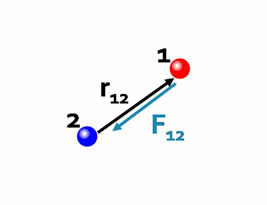 |
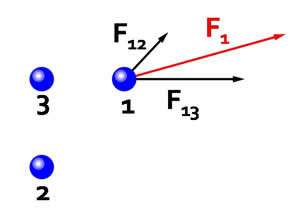
Electrostatic forces are additive, and add vectorially. 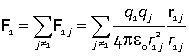 The force on particle 1 is the vector sum of the interaction with charge 2 and the interaction with charge 3. |
 |
Electric forces are attenuated faster through matter than through vacuum.
This is because the charge distribution of matter becomes distorted (polarised) by the presence of a charge.
The force still obeys Coulomb's law, but the constant of proportionality is altered
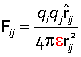
The permittivity of the medium ε > ε0, indicating that the force falls off more rapidly with increasing distance than in a vacuum.
The units of ε are the same as those of ε0.
For convenience we introduce a scaling factor called the dielectric constant or relative permittivity to measure how much faster the forces fall off with distance than in a vacuum. The dielectric constant εr is defined by ε = εrε0, and it therefore has no units, i.e. it is a pure number.
| medium | εr |
| vacuum | 1 |
| air | 1.0006 |
| cyclohexane (l) | 1.89 |
| ethanol (l) | 24 |
| dimethyl sulfoxide (l) | 47 |
| water (l) | 78 |
Example - the force between two elementary charges
Calculate the force between two elementary charges (e.g. two protons) separated by 1.00 nm in water.
q1 = q2 = 1.602×10-19 C. r = 1.00×10-9 m. Hence F = 2.96×10-12 N.