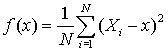
Take a binomial expansion of the square
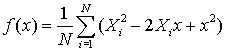
Proof that mean squared deviations are minimised by the sample mean.
Define a function to equal the mean of the squared deviations of a sample from a variable x.
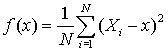
Take a binomial expansion of the square
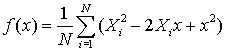
Now use the definition of the sample mean
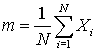
to rewrite this equation in the form
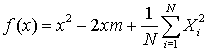
where N is the number of measurements in the sample and Xi is the value of the ith measurement.
Finally minimise this function with respect to the variable x.
![]()
which has the solution x = m.
Thus the function f(x), measuring the mean squared deviations from x has its minimum value at the sample mean m and hence the mean squared deviations about any other point, including the true mean, must be larger than s2 = f(m). QED.