Level 0 (green)- this is basic material that you have probably encountered already, although the approach may be slightly different. No prior knowledge is assumed.
Precision may be measured by repeating the experiment several times.
Estimates of precision should be interpreted as estimates of the precision of a typical measurement.
This section deals with the following measures of precision, some of which require the definition of the sample mean: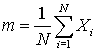
where N is the number of measurements in the sample and Xi is the value of the ith measurement.
By far the most useful of these is the standard deviation
The section finishes with a discussion of how precisely the sample mean reflects the "true" mean.
The range covered by the measurements that have been taken.
For example, here is a set of results from 5 students who have performed a gravimetric analysis of chloride by precipitating silver chloride and weighing the precipitate.
4.815 g, 5.213 g, 4.956 g, 5.012 g, 4.901 g.
The highest measurement is 5.213 g and the lowest is 4.815 g, so the total range of the data is 0.398 g.
The correct value presumably lies somewhere inside this range, and one might be tempted to put it halfway between these values, at 5.014 g but this would only use two of the five measured values.
It would be better to use the median value 4.956 g or the mean value, 4.979 g.
From the range of values the precision of a typical measurement is estimated as ±0.20 g.
The disadvantage of this method is that it does not measure the typical error because it relies entirely on the outlying measurements. It can easily be distorted by an anomalous outlier.
Some measurements lie above the mean (positive deviations from the mean) and some lie below the mean (negative deviations). From the definition of the mean these deviations average to zero.
But if we average the absolute (positive) values of the deviations we get a useful estimate of precision.
| mass / g | deviation / g | |
4.815 |
-0.1644 |
|
5.213 |
+.2336 |
|
4.956 |
-.0234 |
|
5.012 |
+0.326 |
|
4.901 |
-.0784 |
|
| mean | 4.9794 |
0.1065 |
Notice that the mean absolute deviation (0.1065 g) is smaller than the full range of deviations because it measures a typical deviation rather than the maximum deviation.
The mean absolute deviation is useful, but is not very convenient to manipulate mathematically.
Another way of making sure that the quantities averaged all have the same sign is to square them.
The mean squared deviation of the sample is called the variance.
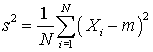
This quantity is not directly comparable with the sample mean because it has the units of the measurement squared.
To obtain a measure of deviations from the sample mean the variance is square rooted. This gives the sample standard deviation.
| mass / g | deviation2 / g2 | |
4.815 |
.02703 |
|
5.213 |
.05457 |
|
4.956 |
.00055 |
|
5.012 |
.00106 |
|
4.901 |
.00615 |
|
| mean | 4.9794 |
0.01787 |
For this set of data the sample variance (mean squared deviation from the sample mean) is 0.01787 g2, and the standard deviation of the sample is 0.1337 g.
The definition of the sample standard deviation is slightly more complicated than indicated here. The quantity defined above is the standard deviation of the sample, i.e. the set of 5 measurements. However, it is not the best estimate of the standard deviation of an individual measurement.
If you calculate the standard deviation of these 5 measurements using the Excel function stdev() you will get a slightly larger answer, 0.1495 g, which is a better estimator for the standard deviation of a typical measurement. The reason for this is that the standard deviation defined above measures deviations from the sample mean, but what you really want is a measure of deviations from the true mean. It is easy to prove that the mean square deviation from any value other than the sample mean is greater than the sample variance defined above, and hence the mean square from the sample mean will underestimate the mean square deviations from the true mean. For a proof click here.
The underestimate is a factor of (N–1)/N. As a result Excel and most calculators calculate the unbiased estimator of the variance of a measurement,
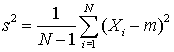
For more details with proofs of the assertions click here. Many calculators provide an alternative function to calculate the true sample standard deviation, and it is important to know which function you are using. In Excel this alternative function is called stdevp().
The standard deviation measures the precision of a single typical measurement.
It is common experience that the mean of a number of measurements gives a more precise estimation than a single measurement. This experience is quantified by the standard error of the mean.
If each measurement has a standard deviation s and the measurements are all independent, then the mean of the N measurements has a standard deviation s/√N. This quantity is called the standard error of the mean. For a proof of this formula see the tutorial on expectations and estimators .
Thus, for the mean to be ten times more precise than a single measurement, 100 independent measurements need to be taken.
In the example the standard error of the mean is 0.067.