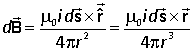Magnetic Field
Level 1 (gold) - this material requires knowledge of vectors, in particular vector products. This is covered in the the first year mathematics for chemists course. Do not attempt this topic until you have mastered the requisite mathematics. You will also find the idea of a line integral useful in tackling this topic.
An electrostatic field E is generated by a point charge following Coulomb's law (see tutorial on electrostatics). A magnetic field is generated my charges in motion, i.e. by an electric current.
There is no current equivalent to a point charge because current must flow from somewhere to somewhere. So instead we consider the magnetic field generated by an infinesimal element of current and then integrate over the whole conductor.
The physical law that permits us to do this is the Biot-Savart law, which, like the Coulomb law, was discovered experimentally:
 |
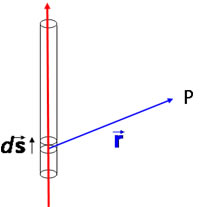Consider a current i flowing through the vector element ds of a conductor. The infinitesimal element of magnetic field at the point P, whose position vector is r relative to the position of ds is given by the Biot-Savart law: |
μ0 is the magnetic constant (permeability of space) and has the value μ0 = 4π×10–7 T m A–1.
The electric and magnetic constants are related by
where c is the speed of light. This relationship is fundamental in the theory of electromagnetic radiation, and will be discussed in the next tutorial.
Suppose that the current i flows through an infinite straight conductor in the +z direction and that the point P lies in the xy plane at the point (x, y, 0).
 |
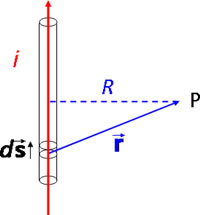Suppose that the current i flows through an infinite straight conductor in the +z direction and that the point P lies in the xy plane at the point (x, y, 0). The element of conductor is at (0, 0, z). The relevant vectors for the Biot-Savart law are |
Hence
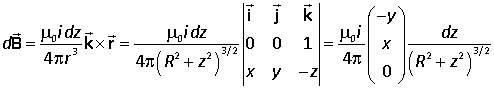Integrating over the whole length of the wire we have
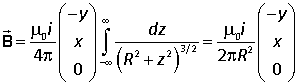
The integral is elementary, and can be evaluated by the substitution
z = R tan θ.
Taking into account the magnitude of the vector (R) the magnitude of the field is seen to be |
 |
We now consider the field due to a cuirrent flowing round a circular loop. Magnetic fields are often generated by passing current through a coil. For simplicity we only consider the point P lying on the axis of the loop.
 |
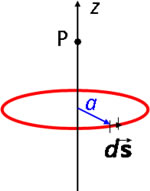Current i flows round a circle of radius a in the xy plane. At a typical point (a cos θ, a sin θ, 0) the vectors for the Biot-Savart law are |
Hence
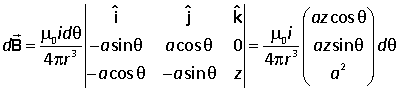
Integrating round the loop,
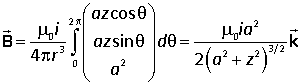
At the centre of the loop z = 0 and
whereas at long distances from the loop, z >> a and
The result is easily generalised to coils containing several loops and solenoids, in which the loops are displaced relative to one another along the z axis. The field of each loop is simply added vectorially. Details can be found in standard Physics texts.
The magnetic field of a current loop at long distances along the axis of the loop,
is reminiscent of the electric field of a dipole p along the axis of the dipole (see electrostatics tutorial)
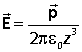
If we define the magnetic dipole moment of a current loop as
then we have
In chemistry the magnetic moment of atoms, nuclei and electrons has a large number of important applications.
The interaction energy of an electric dipole moment with an electric field is given by
and by analogy the interaction energy of a magnetic dipole moment with a magnetic field is
This is the energy that gives rise to the force attracting a compass to point towards the North Pole.
If the magnetic field is in the z direction the interaction energy is
We now apply these ideas to a related problem, that of a charge circulating in a circular orbit. The Biot Savart formula was formulated in terms of current and so we want to interpret this for a single circulating charge.
The current is the rate of passage of charge, which for circular motion is q times the frequency of the circular motion
For a steady circular motion in the xy plane the vector element ds is in the same direction as the velocity. Thus
and so the Biot-Savart law becomes
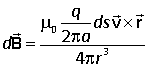
In classical mechanics the angular momentum is defined as
where r is the position vector of the rotating particle. In the Biot-Savart law r is the position vector of the point where the field is measured relative to the position of the moving charge, thus there is a sign difference between these two vectors, and we can reqrite the Biot-Savart law as
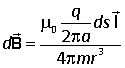
For motion round a circle the element of arc length is
ds = a dθ
and integrating round the circle we find
Equating this with the magnetic field along the axis of a magnetic dipole:
we find an expression for the magnetic moment of the circulating charge
This link between the angular momentum of the circulating charge and the magnetic moment is of the utmost importance in the magnetic properties of atoms.
The orbital angular momentum of an atom has magnitude
and component in the z direction
where l is the orbital quantum number and ml the magnetic quantum number. Thus the orbital magnetic moment has magnitude
and the energy of interaction with a magnetic field is
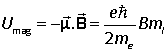
The quantity
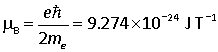
is known as the Bohr magneton
This analysis is significantly complicated by the spin of the electron.
The electron also possesses angular momentum because of its spin. As a result it also possesses a spin magnetic moment.
The additional factor g is very close to 2 (2.002319304386) and its origin is beyond the scope of this course.
Nuclei may also have magnetic moments resulting from their spin. These magnetic moments are generally given in nuclear magneton units, which are similar to Bohr magnetons, except that the mass of the proton is used instead:
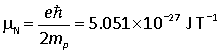
g factors for nuclear spins are not easily predictable.
The interaction of an electronic magnetic moment with an external magnetic field gives rise to a type of spectroscopy (electron spin resonance) which is very important for studying chemical species with unpaired electrons, such a free radicals. The interaction is often known as the Zeeman effect, and is also the origin of fine structure effects in atomic spectra. The interaction of nuclear magnetic moments with an external field is at the origin of NMR spectroscopy.
The vector sum of the orbital and spin magnetic moments of an atom gives an overall electronic magnetic moment to the atom, and of course these two magnetic moments interact with one another (spin orbit coupling). The details of this coupling are complicated. They depend on whether the interaction with the external field or the interaction between the two magnetic moments is stronger. Similar coupling between electronic and nuclear magnetic moments is called hyperfine coupling and gives structure to ESR spectra. And coupling between nuclear spins within the same molecule give spin-spin coupling in NMR, which is one of the most useful effects in the use of NMR to determine molecular structure.
In solids the orbital part of the magnetic moment is often quenched, leaving the "spin only" magnetic moment