Circular motion
This topic deals with a single mass performing a circular motion. We initially start with this simplified version, but it will need to be generalised because some problems in chemistry require a more sophisticated analysis.
We first need a way of defining the position of a particle in its circular motion. We can use Cartesian coordinates, but these are not very convenient, the relationship between x and y on a circle of radius r is
![]()
which has an unfortunate ambiguity of sign.
It is much more convenient to use polar coordinates, r representing the distance to the centre of the circle and θ representing the angle measured anticlockwise from the x axis.
If θ is measured in radians, then the distance travelled by the particle from the x axis, measured round the arc of the circle is s = rθ. (If you are in doubt, remember that a full circle is 2π radians and that the circumference is 2πr.

The characteristic feature of circular motion is that the radius is fixed and only the angle θ moves as time proceeds. θ therefore defines the angular position of the rotating particle.
Having defined angular position it is also useful to define the corresponding angular speed,
![]()
The SI units of ω are radians per second.
If a particle is going round a circle with a constant angular speed, integrating the above equation gives
![]()
Hence we find for the cartesian coordinates

The velocity of the particle is easily found by differentiation
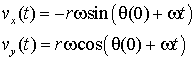
Check that this is perpendicular to the position vector of the particle by taking the scalar product of the two vectors.
Since the position vector is in the radial direction the velocity must be directed along the tangent of the circular motion, and for this reason it is often referred to as the tangential velocity. The magnitude of the tangential velocity is rω.
In the same way, the acceleration of the particle can be seen to have the coordinates
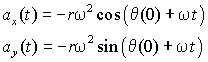
Notice that this is perpendicular to v, but antiparallel to r. The acceleration is directed towards the centre of the circle, and is often called centripetal (centre seeking) acceleration. The magnitude of the centripetal acceleration is rω2.
According to Newton's second law, where there is an acceleration, there is also a force. The force is also parallel to the acceleration (i.e. centripetal) and has magnitude
F = mrω2.
It should not be a surprise that a force is required to make a particle go round in a circle. If there were no force Newton's first law tells us that the particle would travel in a straight line. That the force is towards the centre of the circle should also not be a surprise, the force required to whirl a conker on the end of a bit of string can only be supplied from the string linking the conker to the center of the circle. Similarly the force required to make a satellite move in a circular orbit can only be gravitational attraction to the central planet.
The student will no doubt be familiar with centrifugal force, which seems to fling a person outwards when a car turns a corner. This is a manifestation of Newton's third law. To make you turn the corner the car must supply the centripetal force, otherwise you would carry on in a straight line (not desirable). However by Newton's third law you apply an equal and opposite force on the car, which you perceive as a centrifugal force pushing you against the side of the car. In the frame of reference of the centre of the circle the real force acting is the centripetal force, however in the frame of reference of the person in the car the centrifugal force is equally real, and is used in centrifugation to separate compounds of different masses.
The rotational energy is the kinetic energy of the rotational motion, and so is equal to
![]()
where I = mr2 is called the moment of inertia of the rotating body.
I is a measure of the inertia or resistance of a body to angular acceleration, and is the rotational equivalent of mass as a measure of inertia towards linear acceleration.
If a rigid body is made up of a series of point masses the moment of inertia is additive.
![]()
where ri is the shortest distance from particle i to the axis of rotation. This picture is not a bad approximation for a molecule, where the mass is concentrated in the nuclei. We will look at moments of inertia in more detail in another topic.
We have seen that there is an analogy between linear and rotational motion in the mass (moment of inertia) and the kinetic energy formula. Similarly there is a rotational analogue of the momentum, called the angular momentum. For the simple system we are considering here (uniform motion on a ring) the angular momentum has the simple formula
L = Iω.
The angular momentum is a very important quantity, because, like the linear momentum, in an isolated system it is conserved. This is a vital part of analysing collisions between molecules and also comes into play in spectroscopy.
In many chemical problems the simple analysis in this section is sufficient to form the basis of our understanding of rotating molecules. However, we need to apply the ideas of angular motion and angular momentum to situations that are more complex than a single particle whirling around in a circle with a constan angular speed. Angular momentum is a type of vector, and we need to generalise these ideas.