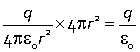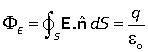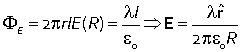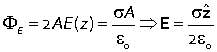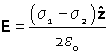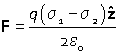Gauss's law
(Level 1)

Point charge Gauss's law Spherical shell Spherical distribution Example Charged wire Charged plane Problems Numerical answers UnitsNext topic Tutorial contents

Gauss's law

Level 1 (gold) - this material has some prerequisites that are covered in the first year mathematics for chemists course. Notably the surface area of a sphere, cylinder etc. The section on Gauss's law is more advanced.

Point charge

Consider a spherical surface (blue) with a point charge at its centre (red). The field lines emanate radially from the charge and so are perpendicular to the sphere. The field times the surface area of the sphere is This quantity is called the electric flux, and denoted ΦE depends only on the charge enclosed by the sphere.

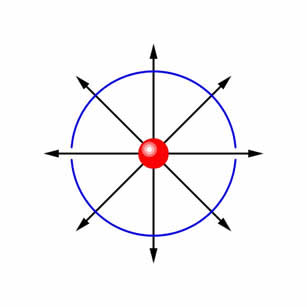This result is an example of Gauss's law, which is a much more general law.

Gauss's law

Warning: this section is more advanced.

Gauss's law states that the electric flux through any closed surface is equal to the charge enclosed by the permittivity. It applies to any charge distribution and any closed surface.

The mathematics behind this are beyond the scope of this undergraduate course. Gauss was one of the greatest mathematicians of the 19th century, and a proper analysis would use all the tools of vector calculus.

A full statement of Gauss's law is Do not panic. In this law each part can be interpreted very simply, even though it is entirely unfamiliar to chemistry undergraduates.

This denotes an integral over the closed surface S, for example a spherical shell of radius r. E denotes the vectorial electric field, and n is a unit vector pointing out from the enclosing surface and perpendicular to it at each point. The integrand is a scalar product representing the component of the electric field perpendicular to the surface.

If the integrand is positive the field is pointing outwards, and if it is negative the field is pointing inwards. If it is zero, the field is parallel to the surface.

You do not need to worry about the details of this, because the only examples we are interested in are those where either

(i) the field is constant and perpendicular to the surface	the integral is equal to EA,
(ii) the field is parallel to the surface	the integral is zero

The field of a spherical shell

Charge q is spread out uniformly over the surface of a spherical shell of radius a (red).

The surface area of the shell is 4πa2 and the charge density is therefore q/4πa2. By symmetry the field is perpendicular to the shell at every point, so the electric flux on any concentric sphere is EA.

To calculate the field at r < a, construct a smaller sphere (blue) with the same centre as the shell. There is no charge enclosed by this sphere and so E = 0.
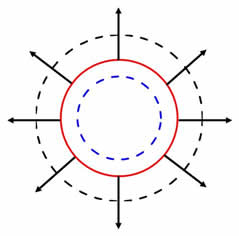To calculate the field at r > a, construct a larger sphere enclosing the shell (black). The enclosed charge is q. From Gauss's law 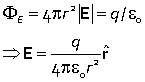as if the charge were concentrated at the origin.

Spherical charge distribution.

Charge q is spread out with a spherically symmetrical density ρ(r) such that

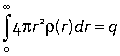
(if the charge density per unit volume is ρ(r) then the amount of charge sandwiched between r and r + dr is 4πr2 ρ(r) dr).

This is an important example in chemistry because it is assumed that the charge distribution in atoms is spherical (the central field approximation), and it is this assumption that permits us to talk about s, p, d orbitals etc., which are only strictly applicable to the H-atom.

Because of the spherical symmetry the field is directed radially outwards and is constant on any sphere with the same centre as the charge distribution.

Hence the field at a radius a can be found from Gauss's law

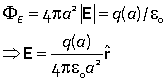
where q(a) is the enclosed charge

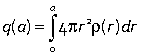
Note that charge outside a does not contribute to the field at a, and the field at a is the same as if all the charge enclosed were concentrated at the origin, a kind of effective nuclear charge.

Example: uniform spherical distribution

Suppose a charge q is evenly spread out within a sphere of radius R. Then the charge density is

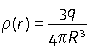
For the field outside the sphere (a > R), the enclosed charge is q and so

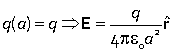
For the field inside the sphere (a < R), we have to do the integral.

Field of a charged wire

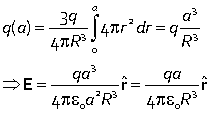
This is rather a physicsy example, but it is of some importance in chemical systems, for example a charged polyelectrolyte (polymer) is modelled like this.

Suppose that charge is spread out uniformly along an infinitely long wire with a charge density of λ per unit length. By symmetry the field is directed radially away from the wire.

Consider a cylinder of length l and radius R. The electric flux through the end faces is zero because the field is parallel to these faces. The electric flux through the cylindrical surface is and the enclosed charge is λl, so applying Gauss's law

Field of a charged plane

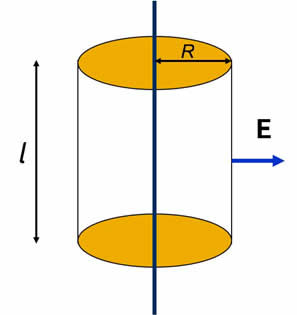This example is also of some importance in chemical systems, for example a charged bilayer is modelled like this, and so is a plane electrode.

Suppose that charge is spread out uniformly on an infinite plane with a charge density of σ per unit area. By symmetry the field is directed directly away from the plane, in the ±z directions.

Consider a cylinder of cross-sectional area A perpendicular to the plane. The electric flux through the side is zero because the field is parallel to this cylinder. The electric flux through the end faces is 2E(z)A, and the enclosed charge is σA, so applying Gauss's law Note that the electric field is independent of distance from the plane.
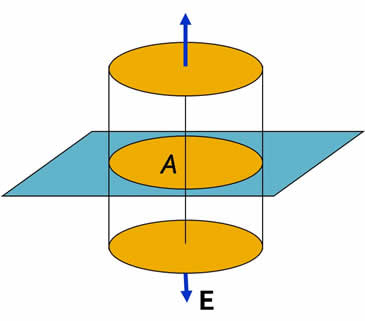If there are two planes with different charge densities, because the fields are additive, between the two planes and in consequence the force on a charged particle between two charged plates is constant,

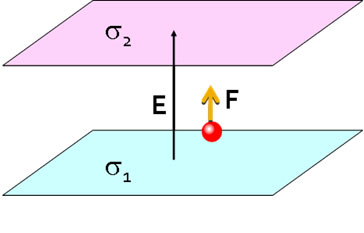These results are useful in many experiments where particles are accelerated through electric fields, such as mass spectrometry and the Millikan oil drop experiment.