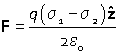Potential and energy
Level 0 (green)- this is basic material that you have probably encountered already, although the approach may be slightly different. No prior knowledge is assumed.
Electrical work in a constant field
How much work does it take to move a charge in a constant electric field. First consider motion parallel to the field.
For a charged particle between two plates with charge densities σ1 and σ2 the force is F = qE, explicitly The work done moving the particle a distance δz parallel to the field is F×δz (force times distance). But moving the particle against the force requires work, and so δw = –F δz. This is the same convention for the sign of work as in thermodynamics (w is work done on the system). |
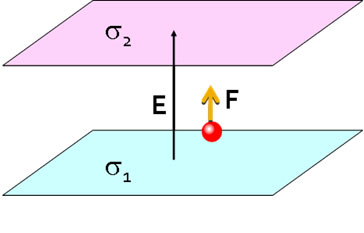 |
If the motion is not parallel to the field, it needs to be resolved into components perpendicular and parallel to the field. The component perpendicular to the field experiences no force and does not conntribute to the work. The component parallel to the field is δr cos θ, hence |
 |
In general the work is an integral along the path followed
| Work done in moving a charge from point A to point B is |
 |
| If the initial and final points are the same, the path is a closed loop and the work done is zero. Such a field is called conservative – there is no loss of energy in moving round the loop |
 |
| The work done in moving a charge from A to B along any path must be the same, as Work on path 1 from A to B must be equal and opposite to work from B to A on path 2: the net result of the two paths is to return to A. | 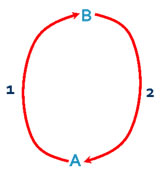 |
Work done in moving a charge from A to B in an electric field is the change in electrical energy of the system.
![]()
This is electrical potential energy, similar to gravitational potential energy. Potential energy is energy stored in the field.
For example, if the electric field is constant in the z direction
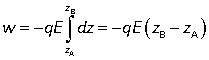
and so in general we can write
![]()
where C is an arbritrary constant, the arbitrary zero of the potential energy scale, which must be defined by a suitable convention.
As a second example, consider the field due to a point charge Q:
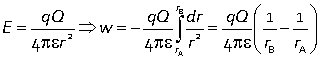
and so in general
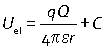
The normal convention is that C = 0, i.e. Uel = 0 at infinite separation from the central charge.
In the two examples given above the potential energy is obtained by integating the force in the direction of the field, for a constant field
![]()
and for a central (spherical) field
![]()
These equations can be inverted: in the first case
![]()
and in the second
![]()
The key result is that the force is minus the gradient of the potential energy.
The results can be generalised: the potential energy relative to the starting point is minus the integral of the scalar product of the force and the path along any path,
![]()
and the force is minus the gradient of the potential energy
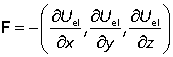
which is often abbreviated
![]()
The relationship between electrical force and field is the same as that between electrical potential energy and potential.
If the electric field at a test charge q is E=F/q then the potential is V = Uel/q.
Since F = –∇Uel, it follows that E = –∇V.
and just as we obtain changes in potential energy by integrating F.dr, from one position to another, so we can obtain changes in potential by similar integration of E.dr.
From the section on the field of the charged plane, the electric field between two charged plates with charge density per unit area σ1 and σ2 is given by
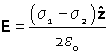
Integrating, we can find the potential relative to plate 1,
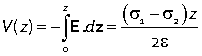
If the plates are separated by a distance d the potential difference between them is therefore
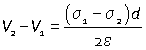
and so the electric field between the plates is
![]()
The SI units for potential are volt (V), which are equivalent to N m C–1 or equivalently J C–1.
A charge released in an electric field is accelerated by that field. The potential energy stored in the field is converted to kinetic energy.
Since the field is conservative there is no dissipation of energy, KE gained = PE lost, and the PE change is the charge on the particle times the change in potential
![]()
This equation is so important that the electronvolt (the energy change if an electronic charge is accelerated through 1 V) is used as a (non-SI) unit of energy on the atomic and nuclear scale.
1 eV = 1.602×10–19 J.
If an ion of charge q is accelerated through a potential difference ΔV it gains a kinetic energy
![]()
if it then flies through flight tube of length d then
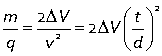
This is the basic principle of time of flight mass spectrometry,