Level 0 (green)- this is basic material that you have probably encountered already, although the approach may be slightly different. No prior knowledge is assumed.
In an important series of experiments in Chicago, Robert Millikan measured the charge on a series of oil drops.
He did this by observing the time taken for a drop to fall at its terminal velocity under the influence of gravity between two fixed levels, this enabled him to deduce the radius of the drop and therefore the drag force operating on it.
He then switched on a potential difference and observed the time required for the same drop to rise between the same levels again, under the competing influences of gravity and the electric force.
By incorporating an X-ray ionisation region into the experiment he could repeat it many times with the same drop, which could take a different charge each time the experiment was repeated
From these experiments Millikan deduced that charge was quantised in units of e, a deduction which probably won him the Nobel prize for Physics in 1923.
Millikan's original papers are quite readable, and the most important one, from 1913, can be found here.
Millikan's experiments were very carefully set up. He chose an oil with a very low vapour pressure so that evaporation of the drops (which would change their size) was minimised. For the same reason he performed repeated experiments with the same drop, as evaporation would be easily detected as a systematic change in the fall time between the two observation levels.
The essential dimensions of Millikan's apparatus are shown in the figure. The observation levels for the falling and rising of a drop were separated by 10.21 mm. The electric field was provided by charged plates separated by 16 mm and charged to a potential difference of about 5 kV, which was constantly monitored. If the droplet has a sufficient positive charge it will rise against gravty when the field is switched on. |
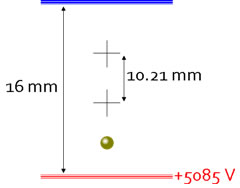 |
In the initial observation the drop falls freely under gravity. If the drop has mass m the gravitational force acting on the drop is mg, where g is the acceleration due to gravity (the gravitational field). This force acts downwards.
The downwards force is slightly altered because the effective mass of the drop m' is its actual mass moil minus the mass of the air it displaces mair, by Archimedes principle. Although the mass of the displaced air is typically 1000 times smaller than that of the droplet, Millikan's measurements were more precise than this, and so this buoyancy correction is necessary. In general, whenever you weigh something in the lab, if you want your mass to be accurate to 3 SF or more, you should make such a correction (or weigh the sample in a vacuum)!
If the density of the oil is ρoil and the density of air is ρair the droplet is spherical and has a radius a then the effective gravitational force on the droplet is
![]()
In Millikan's experiments ρoil was 919.9 kg m–3 and ρair was 1.2 kg m–3. The precision of the density of air is much less vital than that of the oil.
The gravitational field g varies geographically, partly because of fluctuations in the earth's density and partly because of the eath's rotation. In Chicago g = 9.803 kg s–2.
The constant force accelerates the particle downwards, but there is also a frictional force of air resistance, which acts to slow the fall, and increases with the speed of the particle through the air. At the terminal velocity these forces are equal and opposite and the drop falls with a constant speed. This is the case in the Millikan experiment.
In order to interpret the terminal velocity we need a theory of the frictional frag, which was provided by Stokes' law (1851). Stokes analysed the flow of an incompressible fluid around a spherical object and showed that the drag force was (to first order)
![]()
where the minus sign indicates that it acts in the opposite direction to the velocity v. a is the radius of the sphere and η is a quantity known as the viscosity of air.
The derivation of this result, which is important in many areas of chemistry, such as diffusion kinetics, conductivity and sedimentation, comes from the area of Hydrodynamics and is sadly beyond the scope of a first year chemistry course. Interested (and brave) readers could consult H. Lamb's Hydrodynamics (1879, but 6th edition 1994, cambridge UP).
However, this result was not sufficient for Millikan. Air is not an incompressible fluid and so the Stokes result needs to be corrected. The corrected version used by Millikan is
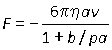
where p is the pressure.
Millikan and his colleagues made careful measurements of the viscosity of air and the constant b. These quantities depend on temperature, and the viscosity was slightly different for each experiment. Typical (modern) values (for drop 6) are
T = 295.98 K
p = 100.82 kPa
η = 1.820×10–5 kg m–1 s–1
b = 7.88 ×10–3 Pa m
The experimental terminal velocity in free fall vg was deduced by measuring the time taken to fall between the two observation levels. For example for drop 6 the mean fall time was 11.879 s (with a standard deviation of 0.040 s in 21 measurements with the same drop). This gives a velocity of 8.594×10–4 m s–1.
Equating the gravitational and drag forces,
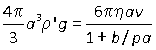
After some rearrangement we obtain a quadratic equation for a
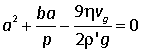
which is easily solved. For the example we are considering this gives a = 2.785 μm.
A rough value can be obtained by neglecting the correction to Stokes' law, i.e. setting b = 0:
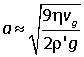
which would instead give a = 2.824 μm.
Now the electric field was switched on. For drop 6 the pd between the plates was 5085 V, giving an electric field of
E = 317.8 kV m–1.
The force on the drop is therefore
![]()
The terminal velocity with the field on vf was measured in the same way, but now in the upward direction, and when combined with the known radius of the particle, this permits the deduction of the charge
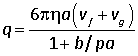
In one of the 21 experiments with drop 6 the rise time was 80.708 s, giving a terminal velocity of 1.265 ×10–4 m s–1 and a charge of 2.943×10–18 C.
Millikan made repeated measurements of this type on many drops. He observed that the charge changed in steps between one passage of the droplet and the next, and that these steps were multiples of a common elementary charge, now known to be 1.602×10–19 C.
In this passage drop 6 carried 18 electronic charges.
It is a good exercise to think about how you might analyse the data to deduce this elementary charge.
Interestingly Millikan's value for the viscosity of air was incorrect by a small amount, and so his deduced value for the elementary charge was also slightly out. It took a surprisingly long time before these small errors were corrected. Everyone who obtained a value slightly different from Millikan seems to have found reasons to correct it incorrectly. This is a warning, remember that the "correct" value may not in fact be correct, even if it has been peer-reviewed and published in the primary literature.