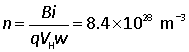Magnetic Force
Level 1 (gold) - this material requires knowledge of vectors, in particular vector products. This is covered in the the first year mathematics for chemists course. Do not attempt this topic until you have mastered the requisite mathematics.
An electrostatic field E can be detected by its action on a charged particle, it exerts a force
![]()
In a similar way a magnetic field B can be detected through its force on a moving charged particle, it exerts a force
![]()
where v is the velocity of the moving particle and q its charge.
At school the vector cross product is often represented using Fleming's left hand rule, in which the thumb represents force, the index finger the field and the middle finger the current. But this is unnecessary if you know how to calculate a vector product.
We can use this equation to deduce the units of the magnetic field,
N C–1 m–1 s = kg s–2 A–1. These units are called Tesla (T).
Example. A Na+ ion moves in the +x direction with a speed of 570 m s–1 in a magnetic field of 9.40 T. Calculate the force and acceleration of the ion (i) if the field is in the x direction, (ii) in the y direction.
Solution. (i) Since the velocity and the field are parallel the force is zero, and therefore the acceleration is also zero. (ii)
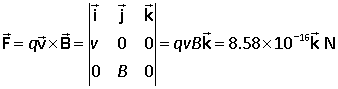
![]()
Suppose that the field B is in the z-direction and is constant. Then a charged particle entering this field with velocity v experiences a magnetic force
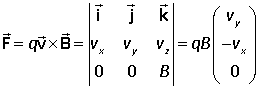
The force is perpendicular to the velocity of the particle, and we therefore expect something like circular motion. To see this we use Newton's second law to obtain the acceleration and split up the equation into three differential equations, each for one component of the velocity:
![]()
The third equation says that vz remains constant, i.e. there is no acceleration parallel to the field.
The first two equations are coupled equations that define circular motion. To see this take the first equation and differentiate again, then use the second equation to substitute for the derivative of vy:
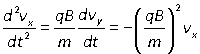
This is the classic second order differential equation for simple harmonic motion, whose general solution can be written
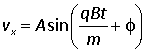
where the amplitude A and the phase φ are arbitrary constants. Hence, from the first differential equation
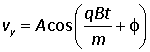
with the same values of A and φ.
Note that
![]()
and so if vz = 0 this is a circular motion centred on the origin with a constant speed A. If vz is not zero the motion is helical.
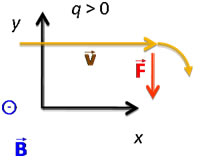
The direction of the circular motion depends on the sign of the charge, as illustrated in the diagram.
 |
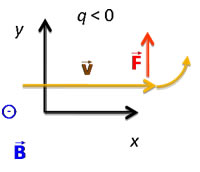 |
The circular symbol in the diagram indicates that the magnetic field is emerging out of the plane pointed towards the observer.
The direction of the circular motion is used by nuclear and particle physicists to identify the particles, see for example CERN.
The radius of the circular motion is also easily found. Since vz remains constant and is not part of the circular motion we set it to zero for the time being. The centripetal force has magnitude
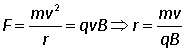
The same result can be found from the angular velocity.
Example. In a magnetic sector mass spectrometer ions are first accelerated through a potential difference V and then enter a magnetic sector, where they undergo a circular motion, as described above. The position at which they strike a detector depends on the radius of this circle.
In the acceleration phase an ion charge q gains kinetic energy qV, and therefore has speed
![]()
in the magnetic sector the ion describes circular motion with radius
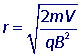
The radius, and therefore the position at which the detector is struck is therefore characteristic of the ration q/m.
J.J. Thomson invented this method for the determination of the charge/mass ratio of the electron.
For example a Na+ ion accelerated through a pd of 1.00 kV gains a speed of 9.16×104 m s–1. It is then introduced into a magnetic field 80.0 mT normal to the motion, and undergoes circular motion of radius 27.3 cm.
The effects of E and B fields are additive: a charged particle in a region containing both experiences a net force
![]()
The most interesting situation is that where the electric and magnetic forces cancel each other out and leave a charged particle undeflected. This requires
![]()
i.e. the electric and magnetic fields must be orthogonal to one another (often referred to as crossed fields). In addition the balance between the fields depends on the velocity of the ion.
Suppose that it is required to select ions of velocity v in the x direction , using a magnetic field B in the y direction. Then the electric field required is
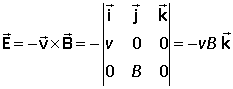
or equivalently, crossed fields E k and B j select ions of velocity –E/B i
This technique is used in modern mass spectrometers as a velocity filter. It was also used by JJ Thomson in his famous experiments on the nature of the electron.
In a conductor conducting electricity, when a magnetic field is applied perpendicular to the conductor the electric field required to cancel the force out is set up automatically. The potential difference required is called the Hall voltage, and the effect is known as the Hall effect.
If a B field is applied to a conductor perpendicular to the current there is a sideways magnetic force on the current carriers. This force produces excess charge carriers on one face and a deficit of charge carriers on the other until a steady state is obtained where the electric force resulting potential difference cancels out the magnetic force. This is the same effect as the velocity filter in the previous section.
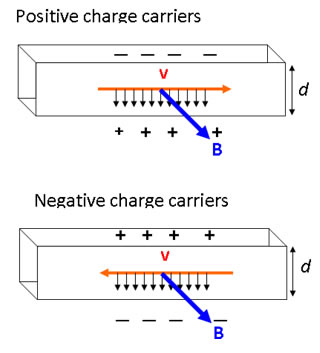 |
Consider a current flowing in the +y direction. The current could be produced by either positively charged particles flowing in the +y direction or by negatively charged particles flowing in the –y direction. The Hall effect allows us to tell the difference. A magnetic field is applied in the +x direction, resulting on a magnetic force on the drifting charge carriers. Thus the PD between upper and lower faces is positive if the charge carriers are negative and negative if the charge carriers are positive. |
The magnitude of the Hall PD is therefore VH = Bvd. It is therefore possible to deduce the drift velocity of the charge carriers from the Hall voltage,
![]()
It is also possible to deduce the density of the charge carriers.
Since i= nAvq,
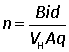
and if the width of the conductor is w then A= wd and
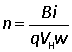
Example. A strip of Cu 1.5 cm wide and 1.0 mm thick conducts electricity. i = 60 A flows in a B =2.5 T and generates VH = 0.74 µV. Calculate the drift velocity and number density of the electrons.
Solution.
![]()