Resistance - Ohm's Law
Level 0 (green)- this is basic material that you have probably encountered already, although the approach may be slightly different. No prior knowledge is assumed.
The definition of resistance is
![]()
which may also be written V = iR and is known as Ohm's law. In this equation V is the potential difference driving the charges through the circuit, i is the current, and R is the electrical resistance.
In chemistry we often also use the conductance, which is the reciprocal of the resistance,
![]()
The SI units for resistance are Ohm (Ω), and since the base units for current and potential difference are A and kg m2 s–3 A–1 (deduced from E = qV), the base units for resistance are Ω = kg m2 s–3 A–2.
But a constant current implies a constant average drift speed, and we know from electrostatics that a charge q in an electric field E experiences a force Eq and hence undergoes a constant acceleration Eq/m, so why should charges in an electrical circuit or an electrolytic cell drift on average with a constant speed?
The answer to this question is treated differently in the different cases of a current in a wire and a current in an electrochemical cell. Indeed, in one case it is more usual to analyse resistance and in the other case conductance.
In a wire of length l with a potential difference V between its ends, suppose that the electron drifts for a random time T before scattering from an atomic centre. During this time it accelerates from a drift velocity of 0 to a drift velocity of aT = EqT/m = qVT/lm. Since all quantities apart from T are fixed, the mean drift velocity is given by
![]()
where τ is the mean time between scattering events.
Hence the current is given by
![]()
and from the definition of the resistance we have
![]()
This equation makes some sense, the resistance is proportional to the length of the wire (and the mass of the current carrier, because of the inverse relation between acceleration and mass), and it is inversely proportional to the density of current carriers, the cross-sectional area of the wire and the mean time between scattering events, during which the charges are accelerated.
Notice that the resistance is proportional to l/A; the quantity
![]()
is therefore a property of the material conducting the electricity, independent of its dimensions, and is called the resistivity.
For a wire the resistivity is
![]()
For example in Cu the resistivity is 1.7 ×10–8 Ω m, and from the above analysis the mean time between scattering events is 25 fs. Using the typical electron speed 1.6×106 m s–1, the electrons travel 39 nm between events, i.e. many atomic distances. (The nearest neighbour distance in Cu is 0.256 nm.
Conductance of ions in solution
In a solution ions are in constant contact with their neighbours, and so the idea of discrete scattering events no longer pertains. An ion between two electrodes separated by distance l with a potential difference V experiences an electric force qV/l. It also experiences a frictional drag as it is pulled by the solution, given by Stokes' law, F = –6πηav, where η is the viscosity of the liquid, a is the radius of the ion and v its velocity . (Compare with the Millikan experiment in the electrostatics tutorial).
The ions drift with a constant velocity when these two forces are in balance: for species i
![]()
Hence, the total current and conductance are given by
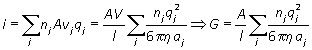
or in terms of molar concentration
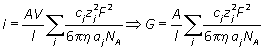
Note that in all this analysis we have ignored any possible interactions between ions, which may affect the electrical properties of the solution. The theory required to discuss these effects is too advanced for this introductory tutorial. (Debye-Huckel-Onsager theory)
The current passed by a solution has contributions from all the species of ions that are mobile, and depends on the electric field V/l, the concentrations of the ions and various properties of the ion (charge, radius) and the solvent (viscosity). The ionic mobility is a quantity that describes the ability of an ion to carry current, it is defined as the drift speed of the ion divided by the electric field driving the motion, ![]()
if Stokes' law can be used for resistance to motion, as above.
Hence, the current and conductance can be expressed in terms or mobilities:
![]()
or in terms of molar quantities
![]()
Because the conductance is a sum of terms from each ionic species involved, it is more natural to analyse conductance rather than resistance for an ionic solution.
However, we note that the conductance of the solution is proportional to A/l in exactly the same way as for a wire, and it is convenient to define a quantity that will only depend on the properties of the solution and not the dimensions of the cell. This quantity
![]()
is known as the conductivity and is simply the reciprocal of the resitivity.
From the analysis above the conductivity of an ionic solution is
![]()
Each ionic species contributes a term proportional to its concentration. This analysis only holds at low concentrations when interactions between ions are unimportant.
Because conductivity is proportional to concentration it is common to define the molar conductivity of an electrolyte, as
![]()
Some books put in an additional factor of 1000, which is simply a conversion factor for the concentration, from mol dm–3 to mol m–3. Keeping units an an integral part of the calculation removes the need for such ad hoc corrections.
For dilute solutions the molar conductivity is to a first approximation a function of the ions present, and the conductivity of a solution may be obtained by scaling up with the concentration of the electrolyte.
For a 1:1 electrolyte the molar conductivity is a sum of the ionic mobilities:
![]()
For electrolytes with different charges, where the stoichiometric coefficient of an ion of charge zj is nj, i.e. cj = nj c, the molar conductivity is
![]()
When calculating and using molar conductivity it is important that the electrolyte be properly specified.