Collisions
Level 1 (gold) - this material requires the concept of vectors, and vector addition, which are covered in the first year mathematics for chemists course.
Collisions are an important part of chemistry, for example molecules in the gas phase can not react with one another unless they collide. Another example is the collisions of gas molecules with the wall of the vessel, which give rise to the phenomenon of gas pressure.
In a collision there is a sudden change in the momentum of the particles involved. This is often assumed to be instantaneous.
The change in momentum of a particle on collision is called the impulse. Of course impulse is a vector.
The simplest collisions to analyse are with a surface because the surface is stationary. There are essentially three types of collision:
- Sticky collisions, in which the particle sticks to the surface.
- Elastic collisions, in which the particle bounces off the surface with the same kinetic energy as before the collision.
- Inelastic collisions, in which the particle exchanges energy with the surface, and may bounce off with less energy or more energy than before the collision.
In a sticky collision, if the initial momentum of the particle is p, its final momentum is zero, hence the impulse on the particle is −p, and the equal and opposite impulse on the wall is +p.
In elastic collision the particle scatters from the wall with the same kinetic energy as it had initially. If the idealised wall is the yz plane the y and z components of the particle momentum are unaltered, and the x component, px, (perpendicular to the wall) is reversed. The impulse on the particle is therefore −2px and the impulse on the wall is +2px. The force arising from this impulse is the molecular origin of gas pressure (see problems).

Inelastic collisions are more complicated and require knowledge of the amount of energy transferred. Although the kinetic theory of gases uses the idealised assumption that collisions with the wall are elastic, in reality walls are made of atoms and the collisions are not perfectly elastic. However, this does not matter very much for the kinetic theory of gases, because the wall is in thermal equilibrium with the gas the rate of energy loss to the wall and the rate of energy gain from the wall cancel each other out. You can even derive kinetic theory assuming all the collisions are sticky, balancing sticking rate and desorption rate.
When two bodies collide and coalesce into a single collision complex the dynamics are relatively straightforward.
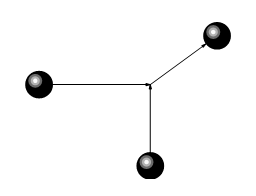
If there is no external force acting on the collision the total momentum before the collision is the same as the total momentum after the collision (see tutorial on Newton's laws). In addition it is obvious that the mass of the collision complex is the sum of the masses of the colliding particles. Hence
![]()
The left hand side is a vector addition.
This permits us to calculate the velocity vector of the collision complex:
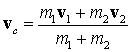
The kinetic energy of the collision complex is always smaller than the sum of the kinetic energies of the colliding particles (click for a proof). The "lost" energy is converted to some kind of internal motion of the collision complex (rotation, vibration etc.)
In analysing collisions it is useful to transform the coordinates so that instead of considering the position vectors of the two collision partners we consider instead the motion of the centre of mass of the system and the vector from one particle to another.
The centre of mass (centre of gravity) of the system is
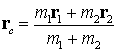
and it therefore moves with a velocity
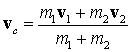
(compare this with the velocity of the collision complex above).
Tote that the total momentum of the whole system can be expressed as Mvc, where M is the total mass of the two particles. Because of the conservation of momentum this quantity remains constant throughout the collision. The collision only affects the relative velocity,
![]()
The velocity of particle 1 relative to the centre of mass is obtained by the vector difference
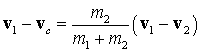
(a little bit of cancellation has been done here)
and similarly for the velocity of particle 2 relative to the centre of mass
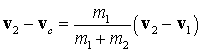
Note that these vectors are antiparallel, parallel to the relative velocity respectively. Even better, the momenta of the two particles in the centre of mass system are equal and opposite. Defining a reduced mass as
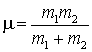
the momenta of the two particles are easily seen to be ±μvr, which we can call ±pr.
The distance between these two parallel trajectories is known as the impact parameter, and often given the symbol b. This would be the closest distance of approach of the two particles if they had no size and no interaction.

The total kinetic energy of the system can also be expressed simply in terms of these two vectors:
![]()
(click here for a proof)
Note that there are no cross terms. The dynamics can be expressed in terms of centre of mass coordinates and relative coordinates, whose dynamics are separable, and independent of each other.
In an elastic collision the kinetic energy before the collision and the kinetic energy after the collision are identical. Although collisions between molecules are not usually elastic (because of the vibrations and rotations of the molecules), collisions between atoms generally are, and important processes such as the Compton effect, and slowing down neutrons in a nuclear reactor are approximately elastic.
Because the centre of mass dynamics (both energy and its momentum) are unaffected by the collision, we can immediately make the following statements for an elastic collision:
- The net momentum in the relative coordinate is zero, i.e. the scattered particles depart on parallel trajectories in the centre of mass system. This is because momentum is conserved and the momentum of the centre of mass is constant throughout.
- The kinetic energy in the relative coordinate after the collision is the same as before the collision. This is because the total energy is conserved in an elastic collision and the part due to the centre of mass motion does not change.
- The magnitude of the relative velocity (relative speed) after the collision is the same as before the collision (of course, the direction will have changed). This is a consequence of the constancy of the kinetic energy of the relative motion.
Worked Example (Prelims 2007)
A neon atom and an argon atom travel towards each other with speeds of 100 m s−1
and 50 m s−1 and their relative atomic masses are 20 mu and 40 mu respectively.
(i) Calculate their relative speeds and relative kinetic energy.
(ii) Calculate the speeds and kinetic energies in the centre-of-mass frame of coordinates.
(iii) Assuming that the atoms undergo an elastic collision calculate their speeds after
the collision.
(Assume that this is a head-on collision so that you only need to consider motion in one dimension).
(i) The velocities of the atoms are 100 m s−1
and −50 m s−1 respectively so their relative speed is the magnitude of the relative velocity, i.e. 150 m s−1.
The reduced mass is 800/60 = 13.3 mu, hence the relative kinetic energy is 1.5 x 105 mu m2 s−2 (you can convert this into J if you want to).
(ii) The centre of mass velocity is (20x100 − 40x50)/(20+40) m s−1 = 0. Hence the speeds in the centre of mass frame are the same as given in the question and the kinetic energies of the two particles are Ne: 1.0x105 mu m2 s−2 and Ar 0.5x105 mu m2 s−2.
(iii) After the collision the relative speed will not have changed, and nor will the relative kinetic energy. Furthermore the total relative momentum must be zero after the collision. Hence we have vAr−vNe = +150 m s−1 and 40 vAr + 20 vNe = 0. Solving the two simultaneous equations the velocities are now vAr=+50 m s−1 and vNe = −100 m s−1.