Momentum and energy
Level 1 (gold) - this material has some prerequisites that are covered in the first year mathematics for chemists course. In particular this tutorial requires a knowledge of vectors and scalar products, and uses these in calculus. A less sophisticated Level 1 tutorial (Energy I) is also available, which is largely limited to one-dimensional motion.
It is notoriously difficult to define energy. There are many different kinds of energy, and it is sometimes possible to interconvert them. Broadly speaking there are two classes of energy important in chemistry: kinetic energy, which depends only on the speeds of the particles in the system and potential energy, which depends only on the locations of the particles in an external field, or relative to each other.
The usual school definition of work is force x distance. However, since force is a vector, and since the force on a particle can depend on its position we need a more sophisticated definition.
If the net force on a particle if F and the particle is moved through an infinitesimal displacement dr, then the work done on the particle is F.dr
The dot signifies the scalar product of the force and the displacement (see maths course). In consequence,
![]()
The integral is a path integral, i.e. the path r followed by the particle must be specified.
Of course in the case of simple one-dimensional motion where the force is constant this definition reduces to the normal school definition.
The kinetic energy is the energy a body has as a consequence of its motion.
The familiar formula is
![]()
It is often useful to express the kinetic energy in terms of momentum instead of speed. Convince yourself that the alternative representation is correct:
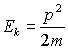
The origin of this formula can be understood by considering the work done in accelerating a free particle from one speed (v1) to another (v2). For simplicity we initially consider motion in one dimension:
![]()
in which Newton's second law has been used for the force, and the infinitesimal displacement has been replaced by v dt.
Now we recognise that
![]()
and that the mass of the particle is a constant
Hence
![]()
The work done is therefore the difference between the initial and final kinetic energies of the particles. This is an example of the conservation of energy: the final kinetic energy of the particle is equal to the initial kinetic energy plus the work done on the particle.
The proof is almost as simple for the general vectorial case:
![]()
(You might like to work out for yourself that the product rule works for the differentiation of a scalar product.)
Potential energy is energy a system has by virtue of its location or its configuration. It can be thought of as stored energy with the potential for being converted to useful work.
The potential energy at a particular location or configuration is the work required to move the system from a location of zero potential energy to the configuration required. It therefore requires a convention for defining zero energy.
The procedure is an idealised infinitely slow procedure so that no conversion to kinetic energy takes place and no energy is lost to friction or any other dissipative process. In this way all the work done is turned into potential energy.
A system left to its own devices will accelerate of its own accord downhill in potential energy (e.g. bodies fall under gravity, opposite charges attract one another.) The work done on the system to store potential energy is done against this natural force F. Hence, in one dimension,
![]()
and in general
![]()
the minus sign indicates that the work is being done against the force.
These integrals are independent of path so that potential energy is a unique function of location or configuration.
This definition can be inverted so that if the potential energy function is known the force on the system can be calculated. In one dimension
![]()
In three dimensions (or more) the result is slightly less obvious. The force is a vector, and so it is necessary to specify all its components. In cartesian coordinates there is an equation like that above for each component of the vector:
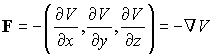
The second equality above is a shorthand abbreviation used in vector calculus for this operation, which is known as the gradient or grad of a multidimensional function.
The important result is that force is minus the gradient of the potential energy - it is not the sign of the potential energy that determines attraction or repulsion, it is the sign of the slope. Forces of this type, which depend only on the position of the particle are called conservative forces.
Harmonic spring
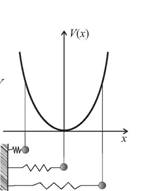
The equation for the potential energy is the parabola
![]()
The zero of potential energy is the minimum of the parabola, and since the derivative and therefore the force are zero at this point, this is the equilibrium position.
The force is given by
![]()
This is proportional to the distance from the equilibrium position, the constant k is known as the force constant, and the minus sign indicates that it is always towards equilibrium. A stretched spring will naturally contract and a compressed spring will naturally expand. This type of potential leads to oscillatory "simple harmonic" motion.
The harmonic potential is often used as an approximate model for the chemical bond, permitting molecular vibrations to be analysed as simple harmonic motion.
Electrostatic potential (Coulomb potential)
The potential energy of interaction of two charges q1 and q2 in a vacuum is
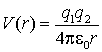
The zero of energy is when the charges are infinitely far apart.
The force is
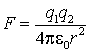
and is directed along the line of centres. (Note the minus sign cancels the minus that comes from the differentiation of r−1). If the charges have the same sign their product is positive, and so the force is positive, i.e. directed towards increasing r, i.e. a repulsion. If the charges have opposite signs the force is attractive.
Other examples will be encountered in the problems.